어텐션(Attention)은 트랜스포머(Transformer) 구조의 핵심 계층(layer)이지만, 대규모 언어 모델(LLM, Large Language Model)과 긴-컨텍스트 애플리케이션(long-context application)의 병목(bottleneck)이기도 합니다. FlashAttention (및 FlashAttention-2)은 메모리 읽기/쓰기를 최소화하여 GPU에서 어텐션 연산을 가속화하는 방법을 개척했으며, 이제 대부분의 라이브러리에서 트랜스포머(Transformer) 학습 및 추론을 가속화하는데 사용되고 있습니다. 이 덕분에 지난 2년 동안 LLM 컨텍스트 길이가 2-4K(GPT-3, OPT)부터 128K(GPT-4) 및 1M(Llama 3)까지 급격히 할 수 있었습니다. 그러나 이러한 성공에도 불구하고, FlashAttention(플래시어텐션)은 최신 하드웨어의 새로운 기능을 아직 활용하지 못했습니다. FlashAttention-2는 H100 GPU에서 이론적 최대 FLOPS(FLoating-point Operations Per Second)의 35%만 활용했습니다. 이 블로그 글에서는 Hopper(호퍼, H100) GPU에서 어텐션 연산을 가속화하기 위한 세 가지 주요 기술을 설명합니다: (1) 워프 특수화(warp-specialization)를 통해 전체 연산과 데이터 이동을 중첩(overlap)하고, (2) 블록-단위 MatMul(Block-wise MatMul) 및 Softmax 연산을 교차로 수행하며, (3) 저정밀도(low-precision) FP8을 위한 하드웨어 지원을 활용하는 비일관적 처리(incoherent processing)입니다.
Attention, as a core layer of the ubiquitous Transformer architecture, is a bottleneck for large language models and long-context applications. FlashAttention (and FlashAttention-2) pioneered an approach to speed up attention on GPUs by minimizing memory reads/writes, and is now used by most libraries to accelerate Transformer training and inference. This has contributed to a massive increase in LLM context length in the last two years, from 2-4K (GPT-3, OPT) to 128K (GPT-4), or even 1M (Llama 3). However, despite its success, FlashAttention has yet to take advantage of new capabilities in modern hardware, with FlashAttention-2 achieving only 35% utilization of theoretical max FLOPs on the H100 GPU. In this blogpost, we describe three main techniques to speed up attention on Hopper GPUs: exploiting asynchrony of the Tensor Cores and TMA to (1) overlap overall computation and data movement via warp-specialization and (2) interleave block-wise matmul and softmax operations, and (3) incoherent processing that leverages hardware support for FP8 low-precision.
이러한 기법들을 활용한 FlashAttention-3을 발표하게 되어 기쁩니다. FlashAttention-3은 FP16에서 FlashAttention-2보다 1.5-2.0배 빠르며, 최대 740 TFLOPS(TeraFLOPS)를 달성합니다. 즉, H100의 이론적 최대 FLOPS의 75%까지 활용할 수 있습니다. FP8에서 FlashAttention-3은 기존(baseline) FP8 어텐션 연산보다 오차가 2.6배 작으며 1.2 PFLOPS(PetaFLOPS)에 가까운 성능을 달성합니다.
We’re excited to release FlashAttention-3 that incorporates these techniques. It’s 1.5-2.0x faster than FlashAttention-2 with FP16, up to 740 TFLOPS, i.e., 75% utilization of H100 theoretical max FLOPS. With FP8, FlashAttention-3 reaches close to 1.2 PFLOPS, with 2.6x smaller error than baseline FP8 attention.
FlashAttention-3는 https://github.com/Dao-AILab/flash-attention에서 확인하실 수 있으며, 논문은 여기에서 확인하실 수 있습니다.
FlashAttention-3 is available at: https://github.com/Dao-AILab/flash-attention
FlashAttention 돌아보기 / FlashAttention Recap
FlashAttention/플래시어텐션은 어텐션 연산을 재배치(reorder)하고 타일링(tiling) 및 재계산(recomputation)을 활용하여 시퀀스 길이에 따른 메모리 사용량을 제곱(quadratic)에서 선형(linear)으로 줄여 속도를 크게 향상시키는 알고리즘입니다. 우리는 타일링을 사용하여 HBM(GPU 메모리)에서 SRAM(빠른 캐시)으로 입력 블록을 불러오고 해당 블록에 대한 어텐션 연산을 수행하며 출력을 HBM에 갱신합니다. 중간 단계의 어텐션 행렬을 HBM에 쓰지 않음으로써 메모리 읽기/쓰기 양을 줄여 연산 시간(wallclock time)을 2-4배 빠르게 하였습니다.
FlashAttention is an algorithm that reorders the attention computation and leverages tiling and recomputation to significantly speed it up and reduce memory usage from quadratic to linear in sequence length. We use tiling to load blocks of inputs from HBM (GPU memory) to SRAM (fast cache), perform attention with respect to that block, and update the output in HBM. By not writing the large intermediate attention matrices to HBM, we reduce the amount of memory reads/writes, which brings 2-4x wallclock time speedup.
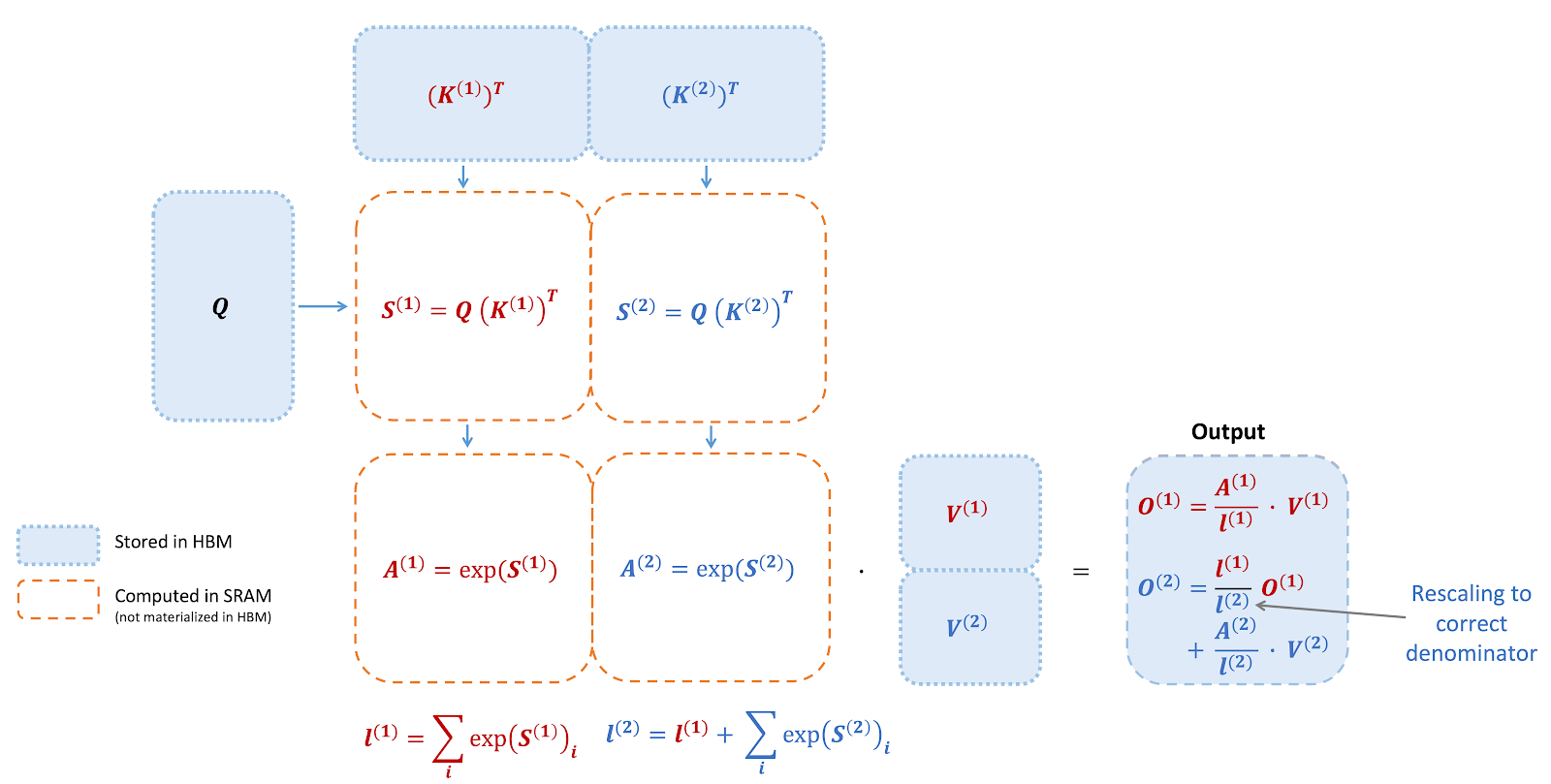
다음은 FlashAttention의 순전파(forward) 연산을 보여주는 다이어그램입니다: 타일링(tiling) 및 softmax 재설계(rescaling)를 함으로써 블록별로 연산을 처리하고 HBM에 읽기/쓰기를 피함으로써 근사치가 아닌 정확한 출력을 얻을 수 있습니다.
Here we show a diagram of FlashAttention forward pass: with tiling and softmax rescaling, we operate by blocks and avoid having to read/write from HBM, while obtaining the correct output with no approximation.
Hopper GPU에서의 새로운 하드웨어 기능 - WGMMA, TMA, FP8 / New hardware features on Hopper GPUs - WGMMA, TMA, FP8
FlashAttention2가 Ampere(암페어, A100) GPU의 이론상 최대 FLOPS의 70%까지 달성할 수 있었지만, Hopper GPU의 새로운 기능을 최대한 활용하여 성능을 극대화하지 못했습니다. 여기에서는 새로운 Hopper-전용 기능 중 일부를 설명하고, 왜 이러한 기능이 중요한지를 설명하겠습니다.
While FlashAttention-2 can achieve up to 70% theoretical max FLOPS on Ampere (A100) GPUs, it does not yet take advantage of new features on Hopper GPUs to maximize performance. We describe some of the new Hopper-specific features here, and why they are important.
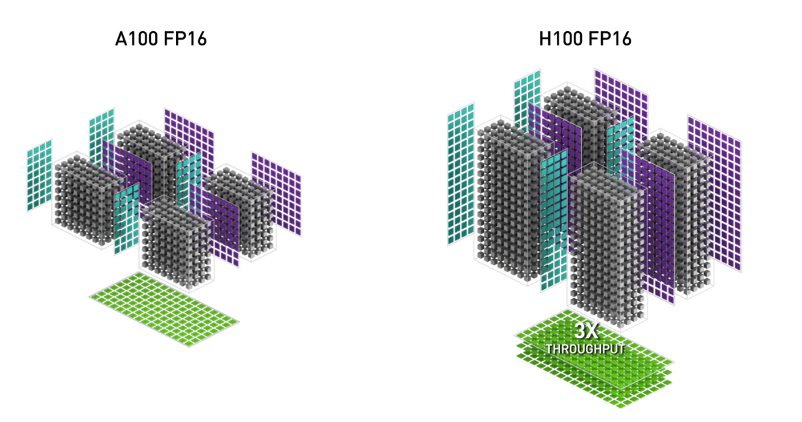
1. WGMMA(Warpgroup Matrix Multiply-Accumulate)는 Hopper의 새로운 텐서 코어(Tensor Core)를 활용하여 Ampere의 이전 mma.sync 명령보다 훨씬 높은 처리량을 제공합니다. (이미지는 H100 백서(whitepaper)에서 가져왔습니다.)
1. WGMMA (Warpgroup Matrix Multiply-Accumulate). This new feature makes use of the new Tensor Cores on Hopper, with much higher throughput than the older mma.sync instruction in Ampere (image from the H100 white paper).
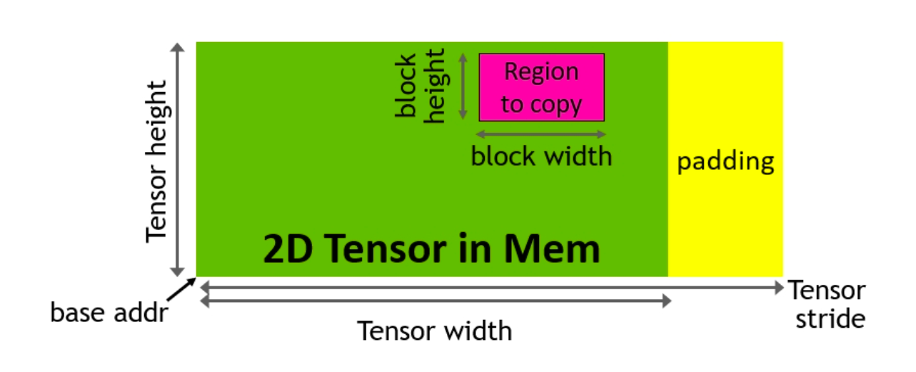
2. TMA(Tensor Memory Accelerator)는 전역 메모리(Global Memory)와 공유 메모리(Shared Memory) 간의 데이터 전송을 가속화하는 특수 하드웨어 장치(special hardware unit)로, 모든 인덱스 연산과 범위-밖(out-of-bound)의 예측을 처리합니다. 이를 통해 레지스터를 확보할 수 있으며, 타일 크기와 효율성을 높이는 데 중요한 리소스를 제공합니다.
2. TMA (Tensor Memory Accelerator). This is a special hardware unit that accelerates the transfer of data between global memory and shared memory, taking care of all index calculation and out-of-bound predication. This frees up registers, which is a valuable resource to increase tile size and efficiency.
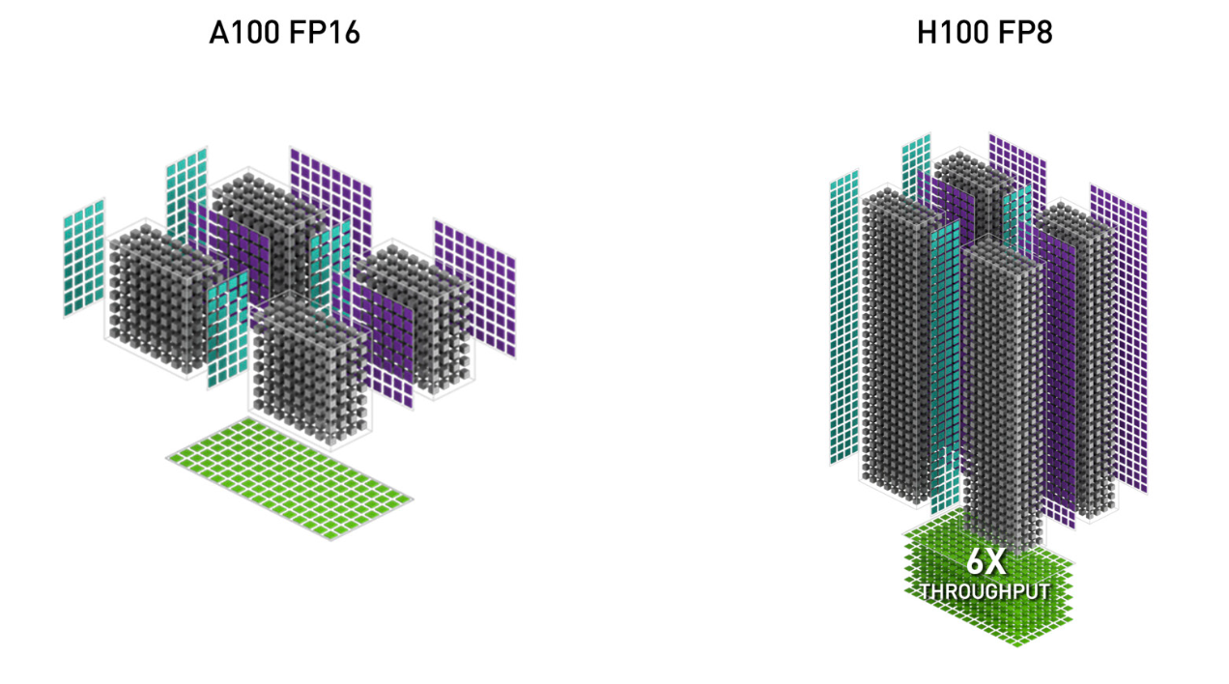
3. FP8의 낮은 정밀도(Low-precision with FP8)에서의 연산은 FP16에서의 연산과 비교하여 텐서 코어 처리량(Tensor Core throughput)을 두 배로 높일 수 있습니다(예: FP16에서 989 TFLOPS, FP8에서 1978 TFLOPS). 그러나 더 적은 비트로 부동 소수점 수(floating point number)를 표현하기 때문에 정확도가 떨어집니다.
3. Low-precision with FP8. This doubles the Tensor Core throughput (e.g. 989 TFLOPS with FP16 and 1978 TFLOPS with FP8), but trades off accuracy by using fewer bits to represent floating point numbers.
FlashAttention-3는 NVIDIA의 CUTLASS 라이브러리의 강력한 추상화(abstraction)를 활용하여 Hopper의 이러한 기능들을 모두 활용합니다.
이러한 새로운 기능들을 사용하도록 FlashAttention을 다시 작성함으로써 이미 FlashAttention-2 FP16 순전파(forward pass)에서 350 TFLOPS에서 540-570 TFLOPS로 성능을 크게 향상시킬 수 있습니다. 그러나 Hopper의 새로운 명령어(WGMMA 및 TMA)의 비동기적 특성(asynchronous nature)은 연산을 중첩(overlap)하고 성능을 더욱 향상시킬 수 있는 추가적인 알고리즘적 기회를 제공합니다. 이 블로그 글에서는 어텐션 연산에 특화된 두 가지 기법을 설명하겠습니다. 별도의 생성자(producer)와 소비자(consumer) 워프(warp)로 TMA와 WGMMA를 수행하는 워프 특수화(Warp Specialization) 기법은 GEMM의 문맥에서 잘 설명해둔 것이 있으며, 여기에서도 동일하게 동작합니다.
FlashAttention-3 makes use of all of these new features of Hopper, using powerful abstractions from NVIDIA’s CUTLASS library.
By rewriting FlashAttention to use these new features, we can already significantly speed it up (e.g., from 350 TFLOPS in FlashAttention-2 FP16 forward pass to around 540-570 TFLOPS). However, the asynchronous nature of the new instructions on Hopper (WGMMA and TMA) opens up additional algorithmic opportunities to overlap operations and thereby extract even greater performance. For this blogpost, we’ll explain two such techniques specific to attention. The generic technique of warp specialization, with separate producer and consumer warps doing TMA and WGMMA, is well-covered elsewhere in the context of GEMM and works the same here.
비동기성: GEMM과 Softmax 중첩하기 / Asynchrony: Overlapping GEMM and Softmax
왜 중첩을 해야 할까요?
Why overlap?
어텐션의 주요 연산은 GEMM(GEneral Matrix Multiplication / 일반적인 행렬 곱셈 연산, Q와 K 사이의 MatMul 연산 및 어텐션 확률 P와 V 사이의 matmul)과 Softmax입니다. 왜 중첩을 해야 할까요? 대부분의 FLOPS가 이미 GEMM에 있는데도요? GEMM이 (WGMMA 명령어를 사용하여 연산하여) 빠르다면, GPU가 부르르르 돌아가야 하지 않을까요?
Attention has GEMMs (those matmuls between Q and K and between attention probability P and V) and softmax as its two main operations. Why do we need to overlap them? Isn’t most of the FLOPS in the GEMMs anyway? As long as the GEMMs are fast (e.g., computed using WGMMA instructions), shouldn’t the GPU be going brrrr?
문제는 최신 가속기들에서 비-행렬곱(non-matmul) 연산이 행렬곱(matmul) 연산보다 매우 느리다는 것입니다. (Softmax의 경우) 지수(Exponential) 연산과 같은 특수 함수는 부동 소수점 곱셈보다 처리량이 매우 낮으며, 부동 소수점 곱하기-더하기(floating point multiply-add) 연산이나 행렬 곱하기-더하기(matrix multiply-add) 연산과 다른 장치(unit)인 다중 함수 장치(multi-function unit)에서 처리(evaluate)됩니다. 예를 들어, H100 GPU SXM5의 FP16 행렬곱 연산은 989 TPLOPS지만, 특수 함수의 경우에는 (256배 적은 처리량인) 3.9 TFLOPS에 불과합니다! 헤드 차원(head dimension)이 128일 때, 지수 연산보다 행렬 연산의 FLOPS가 512배 더 많으며, 이는 지수 연산이 행렬 연산과 비교했을 때 절반 가량의 시간이 소요될 수 있음을 뜻합니다. FP8의 경우 상황은 더욱 악화되어 행렬곱(matmul) 연산 FLOPS는 2배 빠르지만 지수 연산 FLOPS는 동일한 속도를 유지합니다. 이상적으로는 행렬곱(matmul)과 Softmax가 병렬로 동작하는 것이 좋습니다. 텐서 코어(Tensor Core)가 행렬곱 연산으로 바쁜 사이에 다중 함수 장치는 지수 연산을 처리해야 합니다!
The problem is that non-matmul operations are much slower than matmul operations on modern accelerators. Special functions such as exponential (for the softmax) have even lower throughput than floating point multiply-add; they are evaluated by the multi-function unit, a unit separate from floating point multiply-add or matrix multiply-add. As an example, the H100 GPU SXM5 has 989 TFLOPS of FP16 matrix multiply, but only 3.9 TFLOPS (256x less throughput) for special functions! For head dimension 128, there are 512x more matmul FLOPS than exponential, which means that exponential can take 50% of the time compared to matmul. The situation is even worse for FP8, where the matmul FLOPS are twice as fast yet exponential FLOPS stay the same speed. Ideally we want matmul and softmax to operate in parallel. While the Tensor Cores are busy with matmul, the multi-function units should be calculating exponential!
핑퐁 스케쥴링으로 워프그룹 간 중첩 / Inter-warpgroup overlapping with pingpong scheduling
GEMM과 Softmax를 중첩하는 가장 쉬운 첫번째 방법은 아무것도 하지 않는 것입니다! 워프 스케줄러(Warp Scheduler)는 이미 일부 워프(warp)가 차단되는 경우(예. GEMM 결과를 기다리는 경우) 다른 워프(warp)가 실행될 수 있도록 스케줄링합니다. 즉, 아무것도 하지 않아도 워프 스케줄러는 이미 일부 중첩을 수행하고 있습니다.
The first and easiest way to overlap GEMM and softmax is to do nothing at all! The warp schedulers already try to schedule warps so that if some warps are blocked (e.g., waiting for GEMM results), other warps can run. That is, the warp schedulers do some of this overlapping for us, for free.
하지만 일부 스케줄링을 수동으로 수행하여 이를 개선할 수 있습니다. 예를 들어 아래 그림의 Warpgroup 1과 2처럼 (각 4개의 워프로 구성된) 2개의 워프그룹(warpgroup)이 있을 때, 동기화 배리어(synchronization barrier, bar.sync)를 사용하여 워프그룹1이 먼저 GEMM 연산들(예. 첫번째 반복의 GEMM1과 그 다음 반복의 GEMM0)을 수행한 다음, 워프그룹1이 Softmax 연산을 수행하는 동안 워프그룹2가 GEMM 연산을 수행하도록 할 수 있습니다. 이러한 “핑퐁(pingpong)” 스케줄은 아래 그림에 설명되어 있으며, 동일한 색상은 동일한 반복(iteration)을 나타냅니다.
However, we can improve on this by doing some of the scheduling manually. As an example, if we have 2 warpgroups (labeled 1 and 2 – each warpgroup is a group of 4 warps), we can use synchronization barriers (bar.sync) so that warpgroup 1 first does its GEMMs (e.g., GEMM1 of one iteration and GEMM0 of the next iteration), and then warpgroup 2 does its GEMMs while warpgroup 1 does its softmax, and so on. This “pingpong” schedule is illustrated in the figure below, where the same color denotes the same iteration.
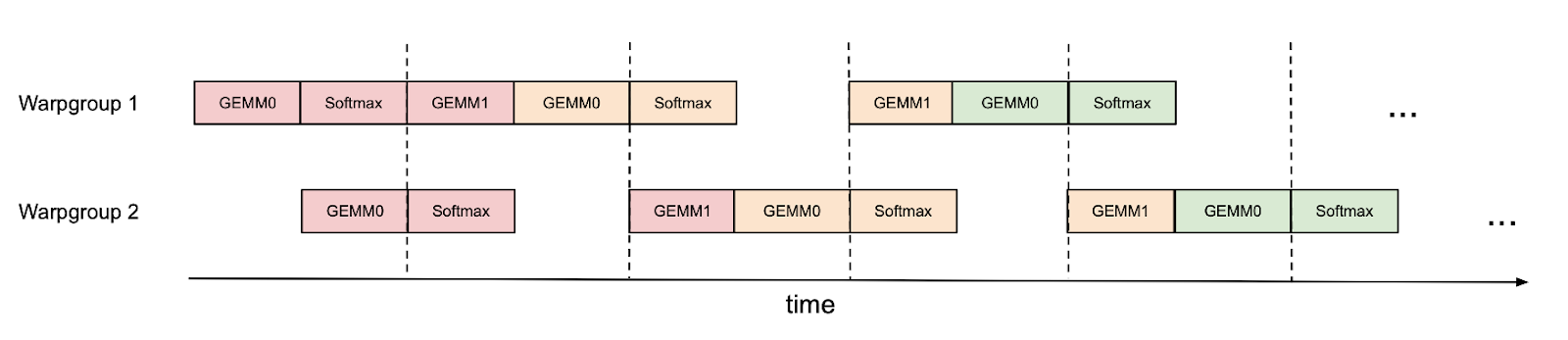
이렇게 하면 다른 워프그룹의 GEMM 연산의 그림자 안에서 Softmax를 수행할 수 있습니다. 물론 이 그림은 대략적인 것으로, 실제 스케줄링은 이렇게 깔끔하지 않습니다. 그러나 핑퐁 스케줄링을 사용하면 (헤드 차원이 128이고 시퀀스 길이가 8K인 경우에) FP16 어텐션의 순전파 성능을 약 570 TFLOPS에서 620 TFLOPS로 향상시킬 수 있습니다.
This would allow us to perform the softmax in the shadow of the GEMMs of the other warpgroup. Of course, this figure is just a caricature; in practice the scheduling is not really this clean. Nevertheless, pingpong scheduling can improve FP16 attention forward pass from around 570 TFLOPS to 620 TFLOPS (head dim 128, seqlen 8K).
GEMM 및 Softmax 연산의 워프그룹 내 중첩 / Intra-warpgroup overlapping of GEMM and Softmax
하나의 워프그룹 내에서도 GEMM과 Softmax의 일부를 중첩할 수 있습니다. 아래 그림에서와 같이, 동일한 색상은 동일한 반복(iteration)을 나타냅니다.
Even within one warpgroup, we can have some part of softmax running while the GEMMs of that warpgroup is running. This is illustrated in this figure, where the same color denotes the same iteration.
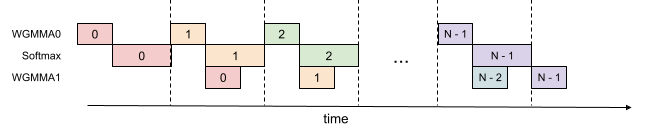
이러한 파이프라인은 FP16 어텐션 순전파 시 처리량을 620TFLOPS에서 640-660TFLOPS로 증가시키지만 레지스터 압력(register pressure)이 높아지는 대가를 치릅니다. GEMM의 누산기(accumulator)와 Softmax의 입/출력을 모두 수용하려면 더 많은 레지스터가 필요합니다. 전체적으로 이 기법이 더 나은 트레이드-오프(favorable trade-off)를 제공한다는 것을 알 수 있습니다.
This pipelining increases throughput from around 620 TFLOPS to around 640-660 TFLOPS for FP16 attention forward, at the cost of higher register pressure. We need more registers to hold both accumulators of the GEMMs, and the input/output of softmax. Overall, we find this technique to offer a favorable tradeoff.
낮은 정밀도: 비일관적 처리로 양자화 오차 줄이기 / Low-precision: reduce quantization error with incoherent processing
LLM 활성화(activation)에는 다른 특징(feature)들보다 훨씬 큰 크기의 이상치(outlier)들이 있을 수 있습니다. 이러한 이상치는 훨씬 큰 양자화 오류(quantization error)를 만들어서 양자화(quantize)를 어렵게 합니다. 양자화 분야(quantization literature)에서 사용하는, Query와 Key에 임의의 직교 행렬(random orthogonal matrix)를 곱하여 이상치를 “퍼뜨려(spread out)” 양자화 오류를 줄이는 비일관적 처리(incoherent processing)를 활용합니다. (예. QuIP) 그 중에서도 (임의의 부호를 사용하는) 하다마드 변환(Hadamad transform)을 사용하는데, 이 방법으로 헤드 차원 $d$에 대해서 어텐션 헤드당 $O(d^2)$ 대신 $O(dlogd)$ 시간에 수행할 수 있습니다. 하다마드 변환은 메모리 대역폭(memory-bandwidth)에 제한이 있으므로, (역시 메모리 대역폭에 제한이 있는) 로터리 임베딩(rotary embedding)과 같은 이전 연산과 “곧바로(for free)” 병합(fuse)할 수 있습니다.
LLM activation can have outliers with much larger magnitude than the rest of the features. These outliers make it difficult to quantize, producing much larger quantization errors. We leverage incoherent processing, a technique used in the quantization literature (e.g. from QuIP) that multiplies the query and key with a random orthogonal matrix to “spread out” the outliers and reduce quantization error. In particular, we use the Hadamard transform (with random signs), which can be done per attention head in $O(d logd)$ instead of $O(d^2)$ time, where $d$ is the head dimension. Since the Hadamard transform is memory-bandwidth bound, it can be fused with previous operations such as rotary embedding (also memory-bandwidth bound) “for free”.
실험을 통해 표준 정규 분포(Standard Normal Distribution)에서 Q, K, V를 생성하면서 (이상치를 나타내기 위해) 0.1%의 항목들이 큰 값을 가지도록 한 경우, 비일관적 처리 시에 양자화 오류를 2.6배 낮출 수 있음을 확인하였습니다. 아래 표에서 수치 오류 비교해두었습니다. 자세한 내용은 논문을 참고해주세요.
In our experiment where Q, K, V are generated from a standard normal distribution but 0.1% of the entries have large magnitudes (to simulate outliers), we found that incoherent processing can reduce the quantization error by 2.6x. We show numerical error comparison in the table below. Please see the paper for details.

어텐션 벤치마크 / Attention benchmark
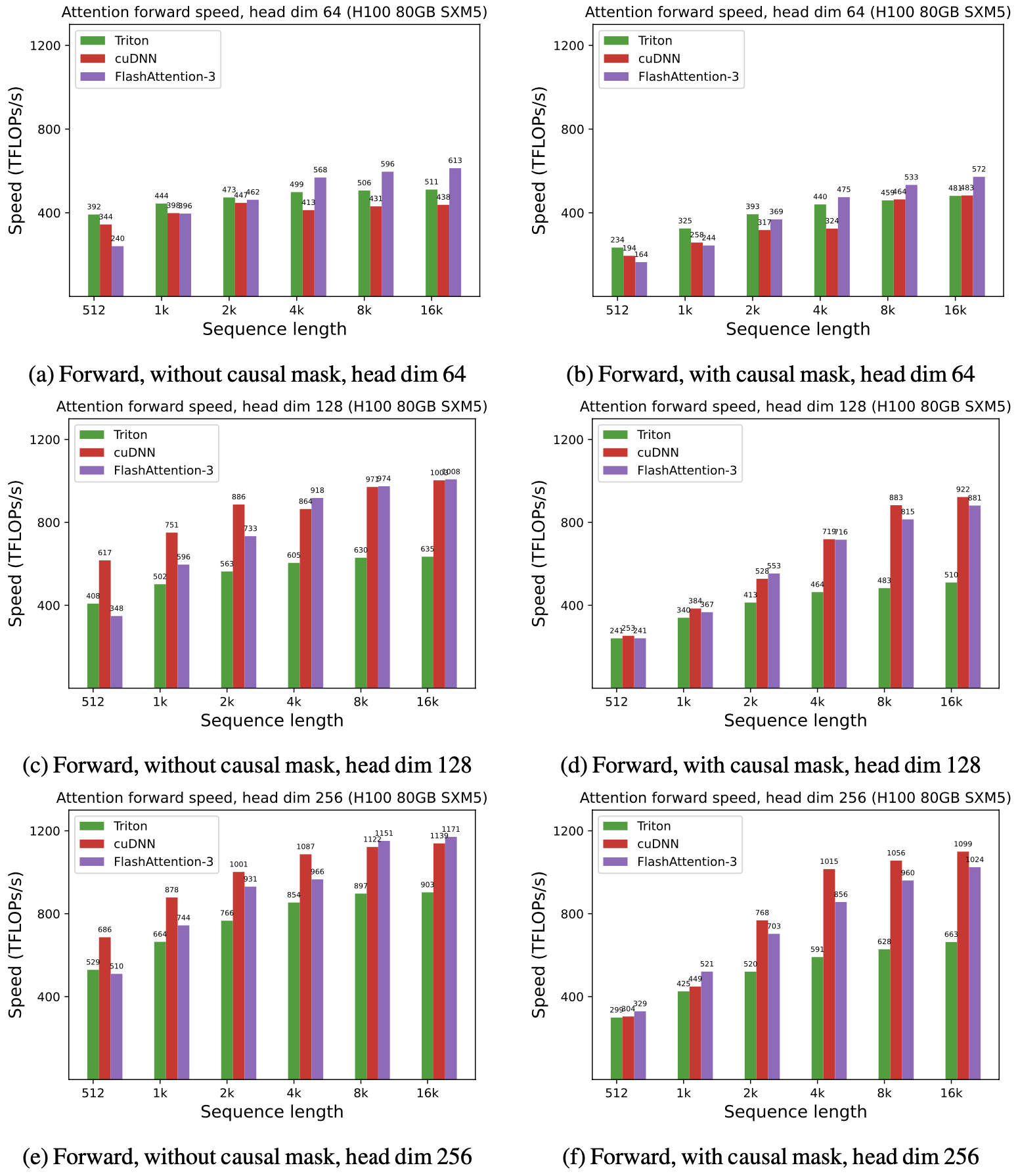
FlashAttention-3 사용 시의 결과를 FlashAttention-2 및 (이미 Hopper GPU의 새로운 하드웨어 기능을 사용 중인) Triton, cuDNN의 구현과 비교해보겠습니다.
We show some results with FlashAttention-3, and compare it to FlashAttention-2, as well as the implementation in Triton and cuDNN (both of which already use new hardware features of Hopper GPUs).
FP16에서, FlashAttention-2 대비 1.6-1.8배의 속도 개선을 확인할 수 있었습니다.
For FP16, we see about 1.6x-1.8x speedup over FlashAttention-2
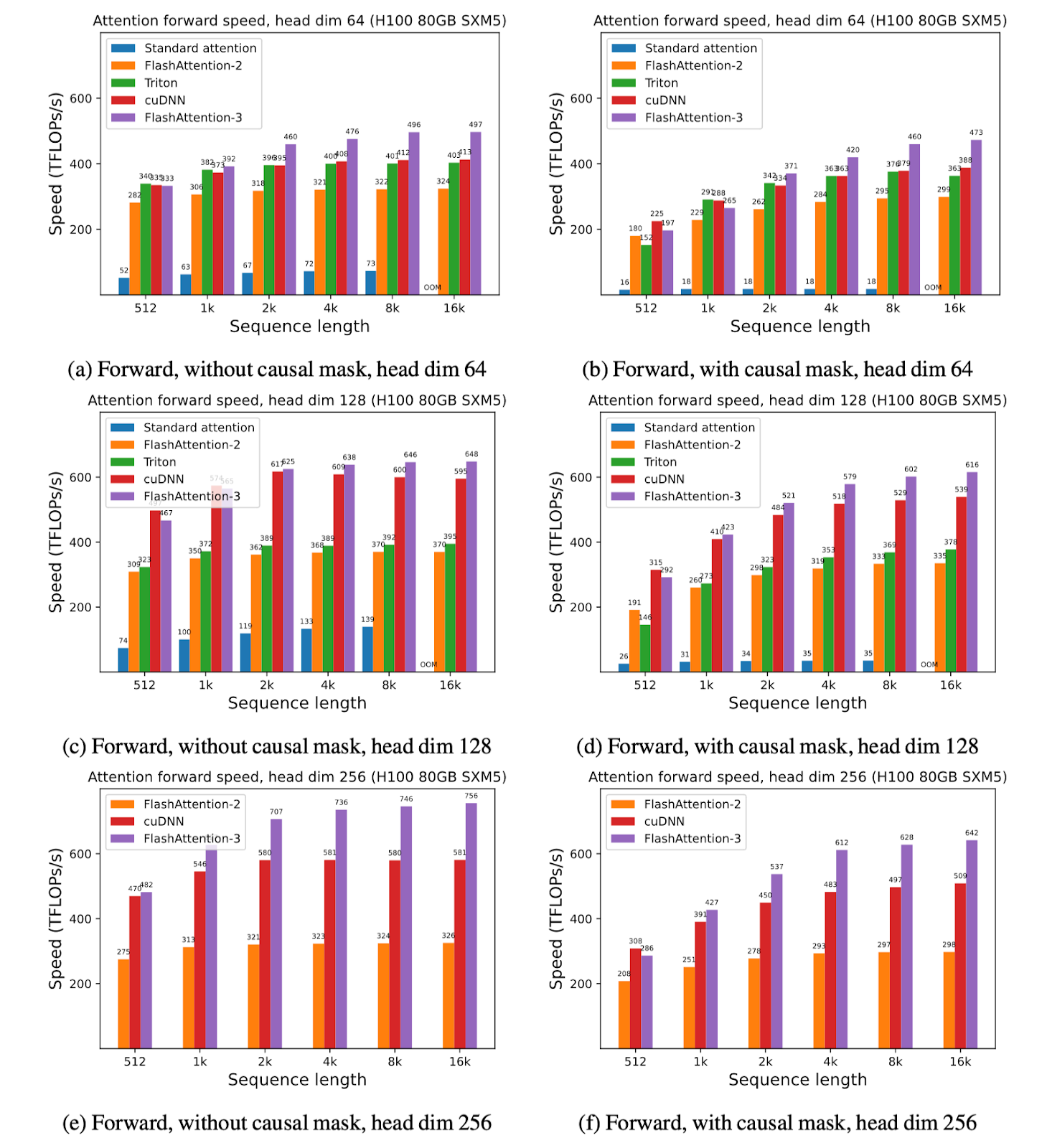
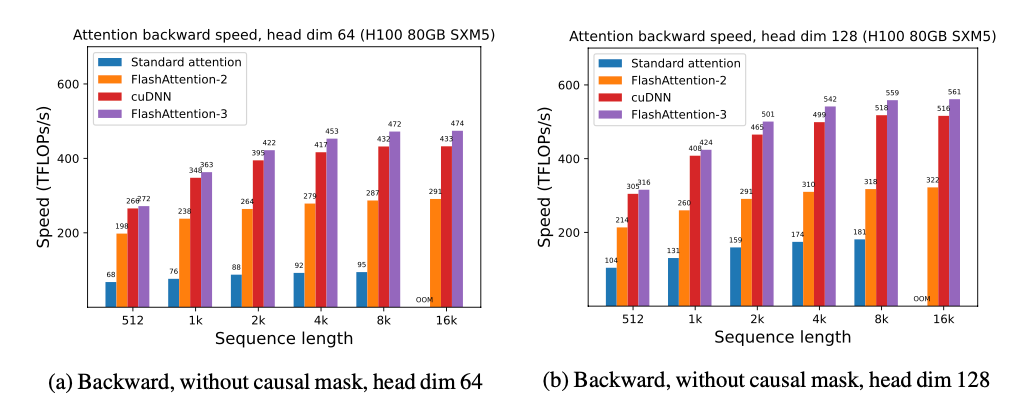
FP8에서는 1.2PFLOPS(PetaFLOPS)에 가까운 속도를 보였습니다!
For FP8, we can reach close to 1.2 PFLOPS!
토의 / Discussion
이번 블로그 글은 Hopper GPU에서 사용할 수 있는 FlashAttention의 최적화 기능 중 일부를 중점적으로 설명했습니다. 가변 길이 시퀀스(variable length sequence)나 영속적인 커널(persistent kernel), FP8에서의 커널 내 전치(in-kernel transpose for FP8)과 같은 다른 최적화들에 대해서는 논문에서 다루었습니다.
This blogpost highlights some of the optimizations for FlashAttention available on Hopper GPUs. Other optimizations (e.g., variable length sequences, persistent kernel, and in-kernel transpose for FP8) are covered in the paper.
지금까지 실행되는 하드웨어를 활용하는 알고리즘을 설계하여 효율성을 크게 향상시키고 긴 컨텍스트와 같은 새로운 모델 기능을 활용할 수 있음을 확인하였습니다. 향후 LLM 추론에서의 최적화 작업과 같은 추가 연구를 기대하며, 이러한 기법이 일반화되어 다른 하드웨어 구조에도 적용될 수 있기를 기대합니다.
We have seen that designing algorithms that take advantage of the hardware they run on can bring significant efficiency gains and unlock new model capabilities such as long context. We look forward to future work on optimization for LLM inference, as well as generalizing our techniques to other hardware architectures.
또한 향후 PyTorch의 릴리즈에 FlashAttention-3가 반영되기를 기대합니다.
We also look forward to FlashAttention-3 being integrated in a future release of PyTorch.
각주 / Notes
덧글 작성 및 공유를 위해 https://pytorch.kr/blog/2024/flashattention-3에 게시된 글이 커뮤니티에도 함께 게시되었습니다.