HyperCloning 연구 소개
대규모 언어 모델(Large Language Model, LLM)의 파라미터 수는 수십억 개에 달하며, 이를 훈련하는 데 필요한 자원은 막대합니다. 예를 들어, 120억 개의 파라미터를 가진 모델을 훈련하는 데 약 72,000 GPU 시간이 필요합니다. 이는 대규모 자원을 소모하게 되어 금전적, 환경적 부담을 증가시킵니다. 소규모 언어 모델(Small Language Model, SLM)은 훈련 비용이 적지만, 그 성능은 대형 모델에 미치지 못합니다.
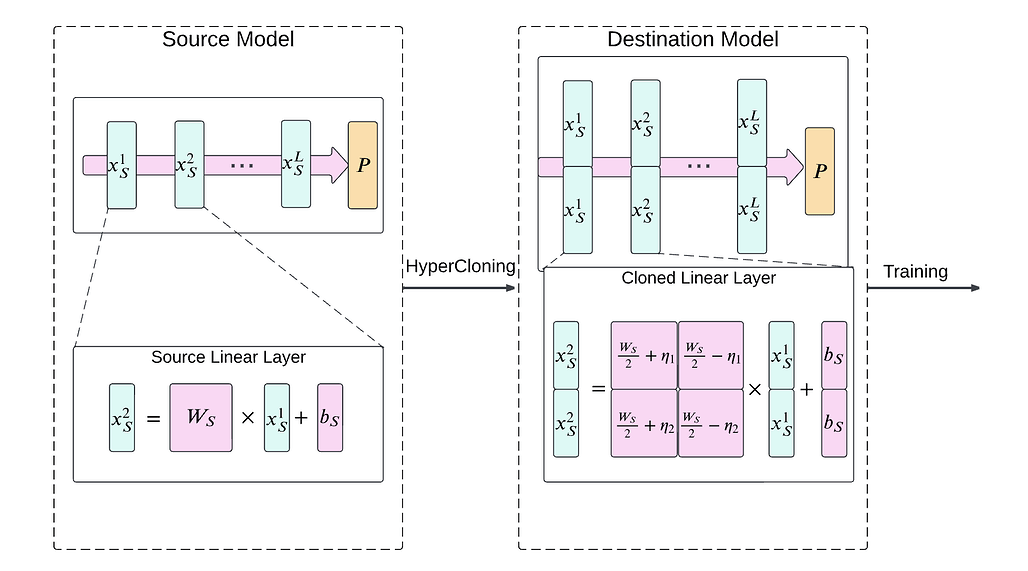
본 논문은 이러한 두 가지 문제를 해결하기 위해 작은 모델을 사전 훈련하고, 이를 더 큰 모델로 확장하여 초기화하는 새로운 기법인 **하이퍼클로닝(HyperCloning)**을 제안합니다. 하이퍼클로닝을 사용하면 대형 모델이 학습 시작부터 작은 모델의 기능을 계승하여 높은 초기 성능을 가지게 됩니다. 이 방법은 전체적인 학습 시간을 단축하면서도 더 높은 최종 성능을 얻을 수 있는 전략을 제공합니다.
HyperCloning 연구 개요
하이퍼클로닝(HyperCloning)은 작은 모델에서 큰 모델로의 지식 전이(Knowledge Distillation)를 통해 파라미터 확장을 달성하는 방법입니다. 기존의 모델 확장은 주로 무작위로 파라미터를 초기화하지만, 하이퍼클로닝은 사전 훈련된 작은 모델의 파라미터를 복사하여 더 큰 모델의 초기 파라미터로 사용함으로써 학습의 시작 단계부터 더 높은 성능을 보장합니다.
하이퍼클로닝(HyperCloning)의 주요한 설계 목표는 다음과 같습니다:
하이퍼클로닝의 효과적인 구현을 위해 설정된 몇 가지 설계 목표는 다음과 같습니다.
-
확장 차원(Expansion Dimension): 더 큰 모델은 더 작은 모델과 동일한 레이어 수를 유지하지만, 숨겨진 차원(hidden dimensions)은 더 커야 합니다. 이를 통해 더 큰 모델이 더 많은 정보를 처리할 수 있게 됩니다.
-
기능 보존(Function Preservation): 작은 모델을 더 큰 모델로 변환한 후, 두 네트워크의 최종 레이어에서 출력된 로짓(logits)이 일치해야 합니다. 즉, 확장된 모델이 훈련 초기에 이미 작은 모델의 성능을 유지하여 빠르게 수렴하고 더 나은 최종 정확도를 보장할 수 있도록 합니다.
-
낮은 연산 비용(Low Compute Overhead): 작은 모델에서 큰 모델로의 변환 과정은 단순해야 하며, 복잡한 연산이나 반복적인 업데이트 없이 이루어져야 합니다. 이를 통해 변환 과정에서의 추가적인 연산 부담을 최소화합니다.
-
학습 과정 유지(Unchanged Training Loop): 하이퍼클로닝은 신경망의 초기화 과정에만 관여하기 때문에, 기존의 학습 과정을 변경하지 않고도 적용될 수 있습니다.
HyperCloning 방법론
벡터 클로닝 (Vector Cloning)
하이퍼클로닝의 핵심 개념 중 하나는 벡터 클로닝입니다. 초기화에 사용하는 소형 모델에서 얻어진 숨겨진 표현(hidden representation) x_S \in R^d 은 대상이 되는 대형 모델에서 여러 번 복제되어 확장됩니다. 이를 통해 큰 모델의 숨겨진 표현 x_D \in R^{n \cdot d} 를 얻을 수 있습니다. 수학적으로는 x_S 를 n 번 복제하고 쌓아서 더 큰 차원 x_D = [ x_S, ..., x_S ]^T 로 확장하는 것으로 표현할 수 있습니다.
선형 계층 복제 (Cloning Linear Layers)
선형 계층(Linear Layer)에서는 입력과 출력 차원을 확장하여 복제합니다. 소규모 모델의 선형 계층이 가중치(Weight) W_S 와 편향(Bias) b_S 을 갖고 있다면, 이는 대규모 모델로 확장되며 가중치 W_D 와 편향 b_D 로 변환됩니다. 입력과 출력 벡터 x_S 와 y_S 또한 작은 모델로부터 복제하여 구성합니다.
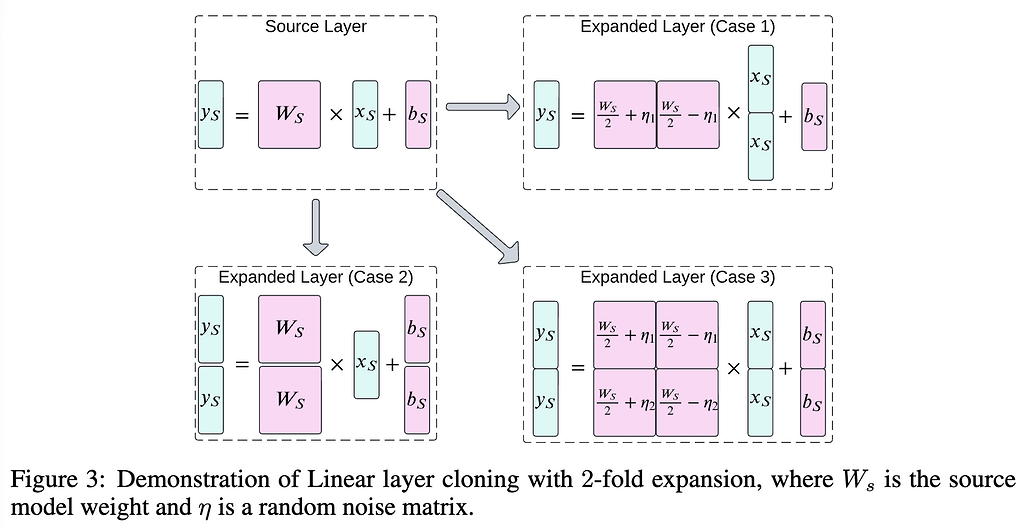
이러한 선형 계층 복제는 일반적으로 3가지 경우로 나눠볼 수 있습니다:
-
Case 1. 입력 차원 확장(Input Dimension Expansion): 입력 벡터가 여러 복제본으로 확장되어 대형 모델로 전달됩니다. (x_D = \begin{bmatrix} x_S \\ x_S \end{bmatrix}) 출력 차원은 그대로 유지되며 (y_D= y_S), 이 과정에서 확장된 가중치와 편향이 입력 벡터와 일치하게 변환됩니다.
-
Case 2. 출력 차원 확장(Output Dimension Expansion): 출력 차원이 확장되며 (y_D = \begin{bmatrix} y_S \\ y_S \end{bmatrix}), 입력은 그대로 유지됩니다. (x_D = x_S) 확장된 출력 벡터는 작은 모델의 출력 벡터 복제본으로 구성됩니다.
-
Case 3. 입력과 출력 차원의 동시 확장(Input and Output Expansion): 입력과 출력이 모두 확장되어 더 큰 차원의 선형 계층이 만들어집니다. (x_D = \begin{bmatrix} x_S \\ x_S \end{bmatrix}, y_D = \begin{bmatrix} y_S \\ y_S \end{bmatrix}) 이는 작은 모델의 입력과 출력 벡터가 복제되어 대형 모델로 확장되는 방식으로, 확장된 가중치와 편향은 작은 모델의 파라미터와 동일한 방식으로 복사됩니다.
가중치(Weight)를 확장할 때는 기존의 사전 학습된 행렬(matrix)을 행 방향과 열 방향 양쪽으로 쌓은(stack) 다음, 입력 차원의 확장 계수(expansion factor) n 으로 나누어 정규화(normalizing)합니다. (\frac{1}{n}) 로 나누어 정규화(normalizing)합니다.
위 3가지 경우에 대해서 가중치 W_D 와 편향 b_D 을 다음과 같이 초기화합니다:
-
Case 1. 가중치와 편향을 각각 W_D = \begin{bmatrix} \frac{W_S}{2} + \eta_1 && \frac{W_S}{2} - \eta_1 \end{bmatrix} 및 b_D = b_S 으로 초기화합니다. 이 때, \eta_1 은 적당한 크기(reasonable magnitude)를 갖는 무작위 텐서(random tensor)입니다. 그 결과 출력 y_D 는 다음과 같습니다:
y_D = W_Dx_D + b_D = \begin{bmatrix} \frac{W_S}{2} + \eta_1 && \frac{W_S}{2} - \eta_1 \end{bmatrix} \begin{bmatrix} x_S \\ x_S \end{bmatrix} + b_S = y_S -
Case 2. 가중치와 편향을 각각 W_D = \begin{bmatrix} W_S \\ W_S \end{bmatrix} 및 b_D = \begin{bmatrix} b_S \\ b_S \end{bmatrix} 로 초기화합니다. 그 결과 출력 y_D 는 다음과 같습니다:
y_D = W_Dx_D + b_D = \begin{bmatrix} W_S \\ W_S \end{bmatrix} x_S + \begin{bmatrix} b_S \\ b_S \end{bmatrix} = \begin{bmatrix} W_Sx_S + b_S \\ W_Sx_S + b_S \end{bmatrix} = \begin{bmatrix} y_S \\ y_S \end{bmatrix} -
Case 3. 가중치와 편향을 각각 W_D = \begin{bmatrix} \frac{W_S}{2} + \eta_1 && \frac{W_S}{2} - \eta_1 \\ \frac{W_S}{2} + \eta_2 && \frac{W_S}{2} + \eta_2 \end{bmatrix} 및 b_D = b_S 으로 초기화합니다. 이 때, \eta_1 및 \eta_2 은 적당한 크기(reasonable magnitude)을 갖는 무작위 텐서(random tensor)입니다. 그 결과 출력 y_D 는 다음과 같습니다:
y_D = W_Dx_D + b_D = \begin{bmatrix} \frac{W_S}{2} + \eta_1 && \frac{W_S}{2} - \eta_1 \\ \frac{W_S}{2} + \eta_2 && \frac{W_S}{2} + \eta_2 \end{bmatrix}\begin{bmatrix}x_S \\ x_S \end{bmatrix} + \begin{bmatrix}b_S \\ b_S\end{bmatrix} = \begin{bmatrix} y_S \\ y_S \end{bmatrix}
이러한 확장 과정에서 노이즈 행렬 \eta 가 더해져 복제된 파라미터에 미세한 변화를 줄 수 있으며, 이는 모델의 다양성을 증가시키는 역할을 합니다.
어텐션 계층 복제 (Cloning Attention Layers)
어텐션 계층(Attention Layer)를 확장할 때에는 MHA(Multi-Head Attention)을 확장하는 2가지 방법이 있습니다:
-
각 어텐션 헤드의 차원 확장(Expanding the dimension of each attention head): 헤드 차원을 확장할 때 각 쿼리(Query)/키(Key)/값(Value) 벡터들은 각각 개별적인 선형 계층(Linear Layer)로 보고 위에서 설명한 것과 같이 확장합니다.
-
어텐션 헤드의 수를 확장(Expanding the number of attention heads): 이 경우는 직관적으로 어텐션 헤드(attention head)를 복제하면 됩니다.
계층 정규화 복제 (Cloning Layer Norm)
일반적으로 Layer Norm에서의 가중치와 편향을 n 번 반복하여 확장된 Layer Norm의 출력과 복제된 버전이 됩니다.
배치 정규화(Batch Normalization)과 RMS 정규화(RMS Normalization), 그룹 정규화(Group Normalization)도 동일합니다.
실험 및 결과
세 가지 오픈 소스 벤치마크 모델인 OPT(Zhang et al., 2023), Pythia(Biderman et al., 2023), OLMO(Groeneveld et al., 2024)을 사용하여 실험을 진행했습니다. 기본 사전 학습된 모델로 OPT-350M, Pythia-460M, OLMO-1B를 선택했고, 하이퍼클로닝(HyperCloning)을 적용하여 더 큰 모델들인 OPT-1.3B, Pythia-1.4B, OLMO-2.9B를 구축했습니다.
무작위 초기화와의 비교 (Comparison to Random Initialization)
HyperCloning을 적용한 모델과 무작위 초기화(random initialization)를 적용한 모델의 학습 수렴 과정을 비교했습니다. 두 경우 모두 학습률, 최적화기 유형, GPU 노드 수, 배치 크기 등 모든 하이퍼파라미터는 동일하게 설정했습니다.
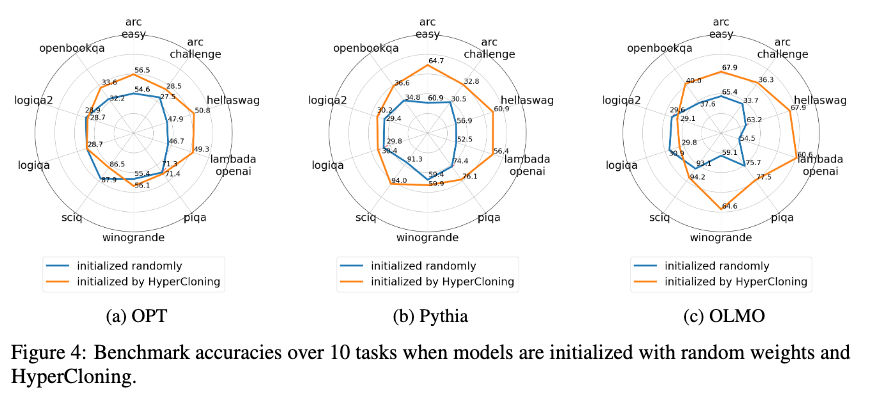
모델의 정확도는 LLM 평가 도구로 널리 사용되는 Harness 프레임워크를 통해 측정했으며, 총 10개의 과제를 대상으로 성능을 평가했습니다. 결과는 아래 그림에서 확인할 수 있듯이, HyperCloning을 사용한 모델이 무작위 초기화에 비해 학습 초기부터 더 빠르게 수렴했으며, 최종 정확도 역시 더 높았습니다. 특히, HyperCloning을 통해 OLMO 모델은 2.4조 개의 토큰을 사용한 사전 학습된 소형 모델의 성능을 전이받아, 2500억 개의 토큰만으로도 높은 성능에 도달할 수 있었습니다.
또한, HyperCloning을 적용한 모델은 학습 초기 단계에서 일시적으로 망각 현상(catastrophic forgetting)을 경험하는 경향이 있었으나, 충분한 학습을 통해 이를 보완할 수 있었습니다. 망각 현상에도 불구하고, HyperCloning은 무작위 초기화 방식보다 훨씬 우수한 성능을 보여주었습니다. 이러한 망각 현상의 원인을 파악하고 해결 방안을 모색하는 것은 HyperCloning을 더욱 발전시키는 중요한 연구 주제가 될 수 있습니다.
HyperCloning의 가중치 대칭성 분석 (Analyzing HyperCloning: Weight Symmetry)
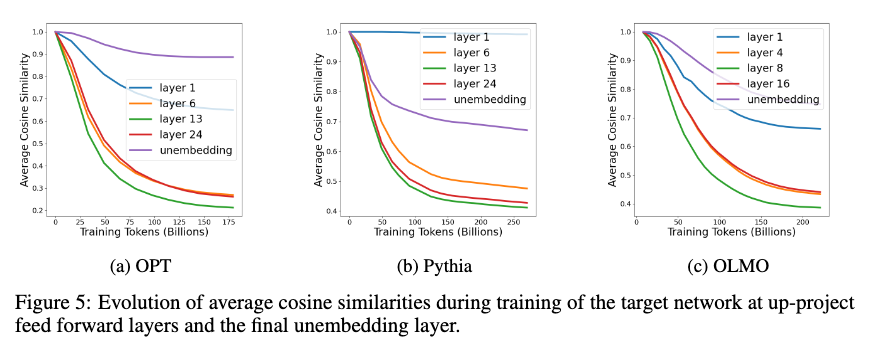
HyperCloning에서는 소형 모델의 가중치를 복제하여 대형 모델을 초기화하기 때문에, 복제된 가중치들이 독립적으로 학습하지 못할 가능성이 있습니다. 그러나, 실험 결과 드롭아웃(dropout)과 같은 무작위 기법이 적용되면서 학습 과정에서 가중치가 자연스럽게 비대칭성을 갖게 되어, 모델이 모든 파라미터를 효과적으로 학습할 수 있음을 확인했습니다.
각 층의 가중치 대칭성은 코사인 유사도를 통해 분석되었으며, 초기에는 대칭성이 높았으나 학습이 진행됨에 따라 대칭성이 감소하는 것을 볼 수 있었습니다. 이는 모델이 학습을 통해 효과적으로 파라미터 공간을 활용하고 있다는 것을 의미합니다.
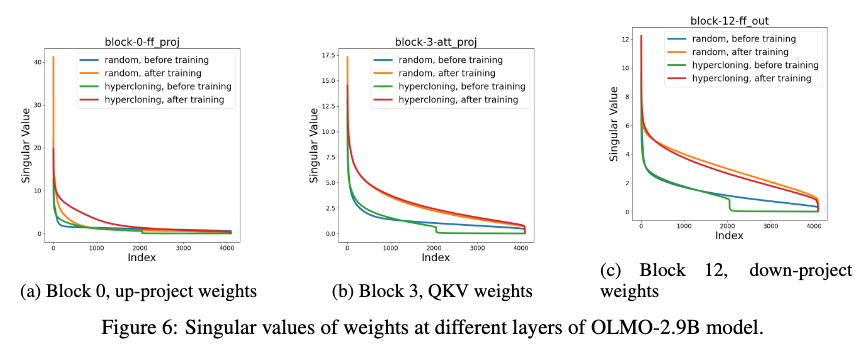
HyperCloning의 주요 구성 요소 분석 (Analyzing HyperCloning: Principal Components)
HyperCloning을 적용한 모델의 가중치 행렬의 주요 구성 요소를 분석한 결과, 초기화 시점에서는 복제된 가중치로 인해 행렬의 랭크가 낮았으나, 학습이 진행되면서 무작위 초기화 모델과 유사한 수준으로 랭크가 높아졌습니다. 즉, HyperCloning을 통해 초기화된 모델도 학습을 통해 충분한 예측 능력을 갖추게 된다는 점을 확인할 수 있었습니다.
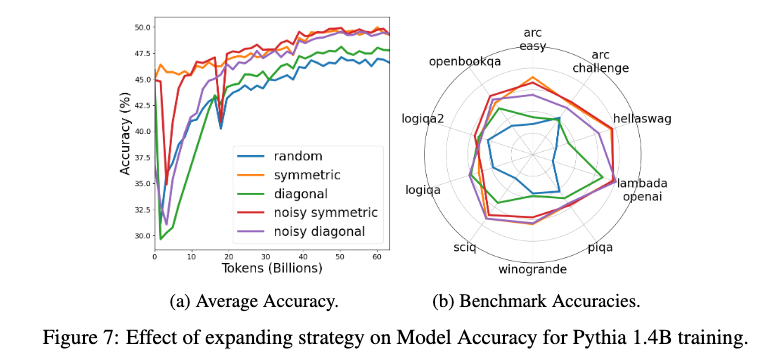
대체 확장 방법 (Alternative Expansion Methods)
HyperCloning에서 제안한 기본 확장 방법 외에도, 다양한 확장 기법을 실험적으로 평가했습니다. 실험한 확장 방법에는 대칭적 확장(symmetric expansion), 대각 확장(diagonal expansion), 노이즈가 포함된 대칭 확장(noisy symmetric expansion), 노이즈가 포함된 대각 확장(noisy diagonal expansion)이 포함되었습니다.
모든 확장 방법이 무작위 초기화보다 우수한 성능을 보였으나, 특히 대칭 확장 방법이 가장 좋은 성능을 기록했습니다. 노이즈를 추가한 확장 방법의 경우 성능 향상이 크지 않았기 때문에, 하이퍼파라미터 튜닝을 피하기 위해 노이즈 없는 대칭 확장 방법이 가장 적합하다고 결론지었습니다.
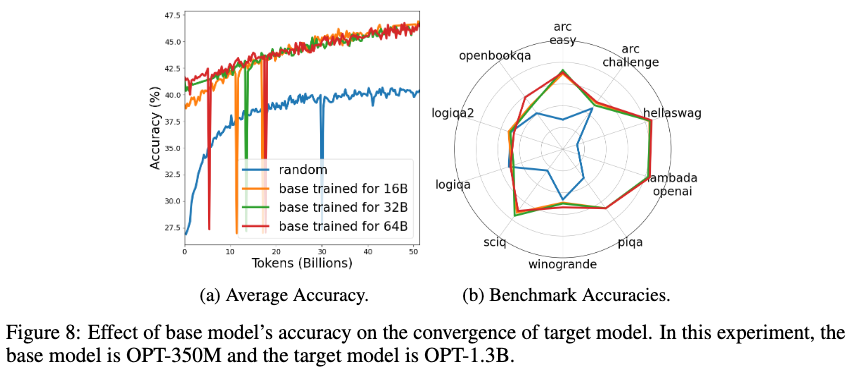
기본 모델 정확도의 영향 (Effect of Base Model Accuracy)
기본 모델의 성능이 HyperCloning을 통해 확장된 모델의 성능에 미치는 영향을 분석한 결과, 기본 모델이 더 높은 정확도를 가질수록 확장된 모델이 학습 초기 단계에서 더 나은 성능을 보였습니다. 하지만 학습이 진행되면서 이러한 차이는 점차 줄어들었으며, 최종적으로는 유사한 성능에 도달했습니다.
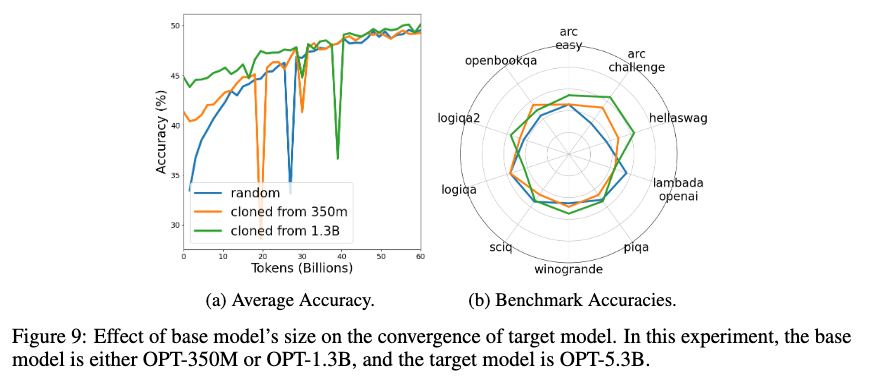
기본 모델 크기의 영향 (Effect of Base Model Size)
마지막으로, 기본 모델의 크기가 확장된 모델의 수렴에 미치는 영향을 분석했습니다. 기본 모델 OPT-1.3B를 기반으로 두 배 확장한 OPT-5.3B 모델을 HyperCloning을 통해 초기화한 경우, 무작위 초기화 모델보다 훨씬 빠르게 수렴했으며, 기본 모델이 더 클수록 수렴 속도가 더 빨라졌습니다. 이는 기본 모델의 크기와 정확도가 HyperCloning의 성능에 중요한 영향을 미친다는 것을 보여줍니다.
HyperCloning 논문
이 글은 GPT 모델로 정리한 글을 바탕으로 한 것으로, 원문의 내용 또는 의도와 다르게 정리된 내용이 있을 수 있습니다. 관심있는 내용이시라면 원문도 함께 참고해주세요! 읽으시면서 어색하거나 잘못된 내용을 발견하시면 덧글로 알려주시기를 부탁드립니다. 
파이토치 한국 사용자 모임
이 정리한 이 글이 유용하셨나요? 회원으로 가입하시면 주요 글들을 이메일
로 보내드립니다! (기본은 Weekly지만 Daily로 변경도 가능합니다.)
아래
쪽에 좋아요
를 눌러주시면 새로운 소식들을 정리하고 공유하는데 힘이 됩니다~ 