- AI 인프라/도구 개발사 ENCORD의 글을, 허락 하에 번역하여 공유합니다.
- ENCORD에서 작성한 원문은 아래 링크를 눌러 보실 수 있습니다.
 이 글에는 ENCORD의 Annotate 서비스 등을 홍보하는 문구가 포함되어 있습니다.
이 글에는 ENCORD의 Annotate 서비스 등을 홍보하는 문구가 포함되어 있습니다.
벡터 유사도 검색은 무엇인가요? / What is Vector Similarity Search?
Akruti Acharya • June 12, 2023 • 5 min read
벡터 유사도 검색(Vector Similarity Search)은 머신러닝의 기본적인 기법으로, 효율적인 데이터 검색과 정확한 패턴 인식을 가능하게 합니다. 추천 시스템, 이미지 검색, 자연어 처리(NLP) 및 기타 어플리케이션 등에서 중추적인 역할을 수행하여 사용자 경험을 개선하고 데이터 기반의 의사결정을 주도합니다.
Vector similarity search is a fundamental technique in machine learning, enabling efficient data retrieval and precise pattern recognition. It plays a pivotal role in recommendation systems, image search, NLP, and other applications, improving user experiences and driving data-driven decision-making.
최인접 이웃 검색(Nearest Neighbor Search)이라고도 하는 벡터 유사도 검색은 고차원의 공간에서 유사한 벡터 또는 데이터 포인트를 찾는데 사용하는 방법입니다. 벡터 유사도 검색은 머신러닝 및 정보검색, 컴퓨터 비전, 추천 시스템 등의 다양한 영역에서 주로 사용됩니다.
Vector similarity search, also known as nearest neighbor search, is a method used to find similar vectors or data points in a high-dimensional space. It is commonly used in various domains, such as machine learning, information retrieval, computer vision, and recommendation systems.
벡터 유사도 검색의 기본 개념은 데이터 포인트를 다차원 공간에서 벡터로 표현하는 것으로, 각 차원은 특정 기능이나 속성에 해당합니다. 예를들어, 추천 시스템에서 사용자의 선호도를 벡터로 표현할 수 있으며, 이 때 각 요소(element)는 특정 항목 또는 카테고리에 대한 사용자의 선호도를 나타냅니다. 마찬가지로, 이미지 검색에서 이미지는 컬러 히스토그램(histogram)이나 이미지 임베딩과 같이 이미지에서 추출한 특징의 벡터로 표현할 수 있습니다.
The fundamental idea behind vector similarity search is to represent data points as vectors in a multi-dimensional space, where each dimension corresponds to a specific feature or attribute. For example, in a recommendation system, a user’s preferences can be represented as a vector, with each element indicating the user’s preferences for a particular item or category. Similarly, in image search, an image can be represented as a vector of features extracted from the image, such as color histograms or image embeddings.
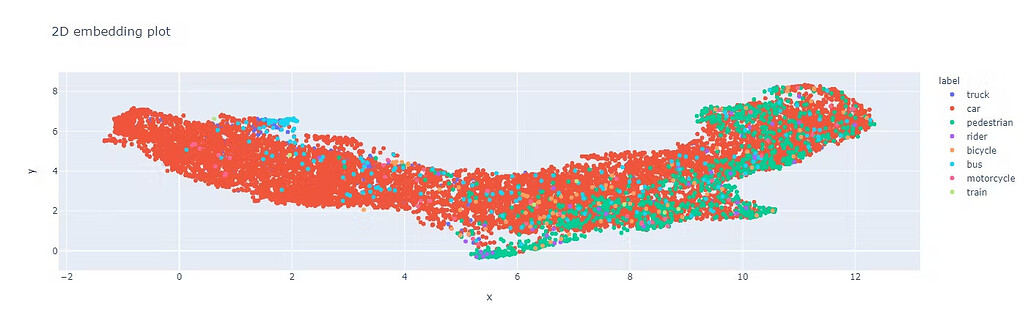
Encord 플랫폼에서 BDD 데이터셋의 임베딩 시각화 예시 / Example of embeddings plot in the BDD dataset using the Encord platform.
이번 글에서는 머신러닝 분야에서의 벡터 유사도 검색의 중요성과 AI 임베딩이 이를 개선하는데 어떻게 도움이 되는지에 대해 설명합니다. 다음 내용들을 다룹니다:
In this blog, we’ll discuss the importance of vector similarity search in machine learning and how AI embeddings can help improve it. We will cover the:
- 고품질 학습 데이터의 중요성
- Importance of high-quality training data
- AI 임베딩을 사용하여 고품질 학습 데이터를 생성하기
- Creating high-quality training data using AI embeddings
- 임베딩의 활용 사례를 보여주는 연구
- Case studies demonstrating the use of embeddings
- AI 임베딩 사용의 모범 사례
- Best practices for using AI embeddings
벡터 유사도 검색이 해결하는 문제는 무엇인가요? / What Problem is Vector Similarity Search Solving?
벡터 유사도 검색은 대규모 데이터셋, 특히 고차원 공간에서 유사한 항목이나 데이터 포인트를 효율적으로 검색해야 하는 문제를 해결합니다. 다음은 벡터 유사도 검색으로 해결할 수 있는 몇 가지 문제들입니다:
Vector similarity search addresses the challenge of efficiently searching for similar items or data points in large datasets, particularly in high-dimensional spaces. Here are some of the problems vector similarity search addresses:
차원의 저주 / Curse of Dimensionality
고차원 공간에서는 데이터의 희소성이 기하급수적으로 증가하여 유사한 항목과 그렇지 않은 항목을 구분하기 어렵습니다. 예를 들어, 512x512 픽셀의 해상도를 갖는 이미지에는 262,144차원의 원시 데이터가 포함되어 있습니다. 이러한 고차원의 원시 데이터(raw data)로 직접 작업하는 것은 연산 비용이 많이 들고 비효율적입니다.
In high-dimensional spaces, the sparsity of data increases exponentially, making it difficult to distinguish similar items from dissimilar ones. For example, an image of resolution 512⨯512 pixels contains raw data of 262,144 dimensions. Working directly with the raw data in its high-dimensional form can be computationally expensive and inefficient.
기존의 검색 방법으로는 이러한 차원의 저주(Curse of Dimensionality) 문제를 효율적으로 처리하기 어렵습니다. 임베딩을 사용하면 이러한 차원을 훨씬 더 낮은, 1024차원 등으로 줄일 수 있습니다. 이러한 차원 축소는 저장 공간을 줄이고, 계산 속도를 향상시키며, 중요한 정보(feature)는 보존하면서 불필요한 정보를 삭제하는 등의 이점을 얻을 수 있습니다.
Traditional search methods struggle to handle this curse of dimensionality efficiently. Using embeddings can reduce these dimensions to 1,024, which is significantly lower. This reduction offers advantages such as decreased storage space, faster computations, and elimination of irrelevant information while preserving important features.
키워드 기반 검색의 비효율성 / Ineffective keyword-based search
키워드 기반 검색이나 일치 검색(exact match)과 같은 기존의 검색 방법은 명시적 키워드가 아닌, 다차원적인 특징(characteristic)을 기반으로 유사도(similarity)를 찾는 시나리오에는 적합하지 않습니다.
Traditional search methods, such as keyword-based search or exact matching, are not suitable for scenarios where similarity is based on multi-dimensional characteristics rather than explicit keywords.
확장성 / Scalability
대규모 데이터셋을 검색하는데는 연산 비용과 시간이 많이 소요될 수 있습니다. 벡터 유사도 검색 알고리즘과 데이터 구조는 검색 공간을 효율적으로 정리(prune)하여, 거리 연산 횟수를 줄이고 유사한 항목들을 더 빠르게 검색할 수 있는 방법을 제공합니다.
Searching through large datasets can be computationally expensive and time-consuming. Vector similarity search algorithms and data structures provide efficient ways to prune the search space, reducing the number of distance computations required and enabling faster retrieval of similar items.
비정형 또는 반정형 데이터 / Unstructured or Semi-Structured Data
벡터 유사도 검색은 이미지, 동영상, 텍스트 문서 또는 센서값 등과 같은 비정형 또는 반정형 데이터를 다룰 때 매우 중요합니다. 이러한 데이터 타입은 자연스럽게 벡토 또는 특징 벡터(feature vector)로 표현되며, 거리 값(metric)을 사용하면 유사도를 더 잘 파악할 수 있습니다.
Vector similarity search is crucial when dealing with unstructured or semi-structured data types, such as images, videos, text documents, or sensor readings. These data types are naturally represented as vectors or feature vectors, and their similarity is better captured using distance metrics.
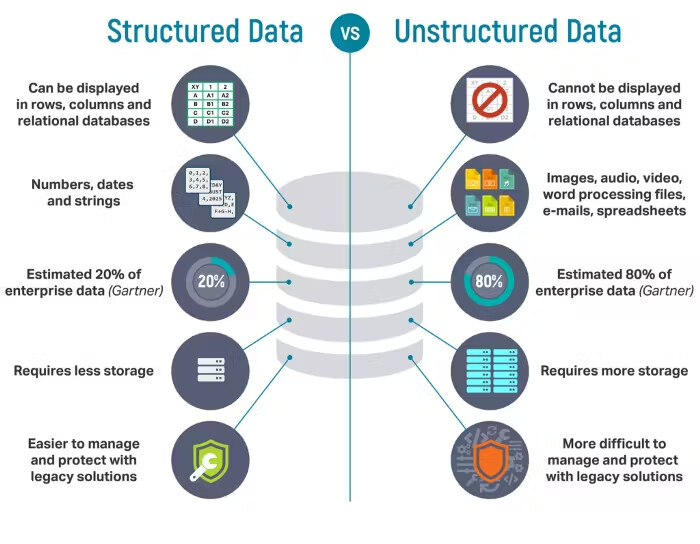
정형 데이터와 비정형 데이터의 차이를 보여주는 그림. 출처 / Illustration showing the difference between structured and unstructured data. Source
벡터 유사도 검색은 이러한 문제들을 해결함으로써 추천 시스템, 콘텐츠 기반 검색, 이상 징후 감지(anomaly detection), 클러스터링 등과 같은 다양한 머신러닝 및 데이터 분석 작업의 효율성과 효과를 향상시킵니다.
By addressing these problems, vector similarity search enhances the efficiency and effectiveness of various machine learning and data analysis tasks, contributing to advancements in recommendation systems, content-based search, anomaly detection, and clustering.
벡터 유사도는 어떻게 동작하나요? / How Does Vector Similarity Work?
벡터 유사도 검색은 3가지 주요한 구성 요소를 포함하고 있습니다:
Vector similarity search involves three key components:
- 벡터 임베딩
- vector embedding
- 유사도 점수 계산
- similarity score computation
- 최인접 이웃(NN) 알고리즘
- Nearest neighbor (NN) algorithms
벡터 임베딩 / Vector Embeddings
벡터 임베딩은 필수적인 특징(essential feature)과 패턴을 갖는 저차원의 데이터로, 유사도 검색 및 머신러닝과 같은 작업(task)에서 효율적인 연산과 분석을 가능하게 합니다. 이는 데이터에서 의미있는 특징(feature)을 추출함으로써 가능합니다. 예를 들어, 자연어 처리(NLP) 분야에서 Word2Vec이나 GloVe와 같은 단어 임베딩 기술은 단어나 문서를 의미 관계(semantic relationship)를 포착하는 조밀하고(dense), 저차원적인 벡터로 변환합니다. 컴퓨터 비전(CV) 분야에서는 합성곱 신경망(CNN; Convolutional Neural Network)과 같은 이미지 임베딩 방법으로 이미지로부터 시각적 특징(visual feature)을 추출하여 고차원 벡터로 표현합니다.
Vector embeddings are lower-dimensional representations of data that capture essential features and patterns, enabling efficient computation and analysis in tasks like similarity searches and machine learning. This is achieved by extracting meaningful features from the data. For example, in natural language processing, word embedding techniques like Word2Vec or GloVe transform words or documents into dense, low-dimensional vectors that capture semantic relationships. In computer vision, image embedding methods such as convolutional neural networks (CNNs) extract visual features from images and represent them as high-dimensional vectors.
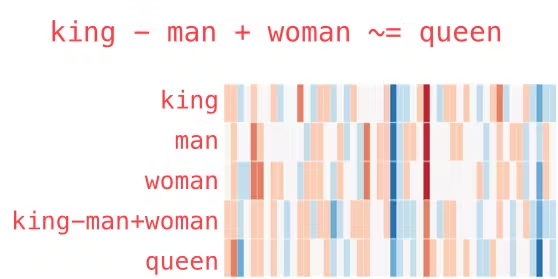
Word2Vec을 사용하여 생성한 벡터 임베딩을 보여주는 예시. 출처 / Example showing vector embeddings generated using Word2Vec. Source
유사도 점수 계산 / Similarity Score Computation
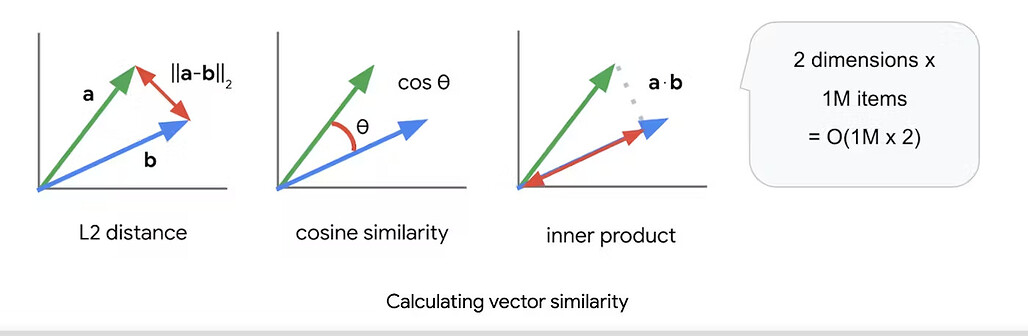
데이터 포인트가 벡터로 표현되면 유사도 점수를 계산하여 두 벡터 간의 유사도를 정량화(quantify)합니다. 유사도 계산에 사용하는 일반적인 거리 기준(metric)에는 유클리드 거리(Euclidean distance), 멘하탄 거리(Manhattan distance), 코사인 유사도(cosine similarity) 등이 있습니다.
Once the data points are represented as vectors, a similarity score is computed to quantify the similarity between two vectors. Common distance metrics used for similarity computation include Euclidean distance, Manhattan distance, and cosine similarity.
유클리드 거리는 공간 내의 두 점간의 직선 거리를 측정하고, 맨하탄 거리는 각 차원의 차이의 절대값의 합을 계산하며, 코사인 유사도는 두 벡터 사이 각도의 코사인 값을 측정합니다. 거리 기준(metric)을 고르는 기준은 데이터의 특성과 사용 중인 어플리케이션에 따라 달라집니다.
Euclidean distance measures the straight-line distance between two points in space, Manhattan distance calculates the sum of the absolute differences between corresponding dimensions, and cosine similarity measures the cosine of the angle between two vectors. The choice of distance metric depends on the characteristics of the data and the application at hand.
최인접 이웃(NN) 알고리즘 / NN Algorithms
최인접 이웃(NN; nearest neighbor) 알고리즘은 주어진 질의 벡터(query vector)의 가장 가까운 이웃(들)을 효율적으로 검색하는데 사용합니다.이 알고리즘은 검색 속도를 크게 향상시키기 위해 정확도를 다소 희생(trade-off)합니다. 대규모의 유사도 작업을 위해 여러 ANN(Approximate Nearest Neighbor; 근사 최인접 이웃) 알고리즘이 개발되었습니다:
Nearest neighbor (NN) algorithms are employed to efficiently search for the nearest neighbors of a given query vector. These algorithms trade off a small amount of accuracy for significantly improved search speed. Several ANN algorithms have been developed to handle large-scale similarity tasks:
k-최인접 이웃(kNN) / k-Nearest Neighbors (kNN)
kNN 알고리즘은 데이터셋의 모든 벡터들과의 거리를 비교하여 질의 벡터(query vector)로부터 가장 가까운 이웃 k개를 검색합니다. 무차별 검색(brute-force search)을 하거나 k-d 트리 또는 볼 트리(ball tree)와 같은 자료구조를 사용하여 최적화할 수 있습니다.
The kNN algorithm searches for the k nearest neighbors of a query vector by comparing distances to all vectors in the dataset. It can be implemented using brute-force search or optimized with data structures like k-d trees or ball trees.
나이브 k-인접 이웃(kNN) 알고리즘은 연산 비용이 많이 들고 복잡도가 O(n^2) 이며, 여기서 n 은 데이터 포인트의 개수입니다. 이는 각각 데이터 포인트 쌍 사이의 거리를 계산해야 하므로 n*(n-1)/2 번의 거리 계산을 해야 하기 때문입니다.
Naive k-nearest neighbors (kNN) algorithm is computationally expensive, with a complexity of O(n^2), where n is the number of data points. This is because it requires calculating the distances between each pair of data points, resulting in n*(n-1)/2 distance calculations.
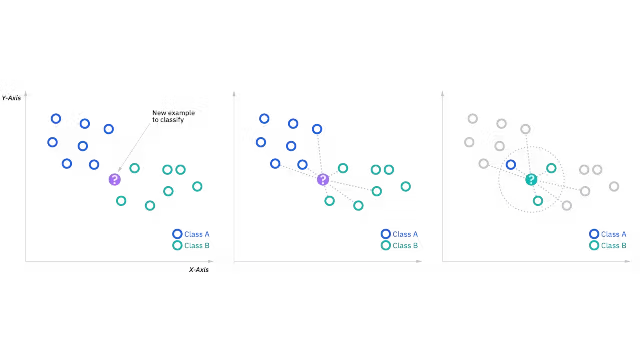
kNN 알고리즘. 출처 / kNN algorithm.Source
공간 파티션 트리 및 그래프(SPTAG) / Space Partition Tree and Graph (SPTAG)
SPTAG는 벡터를 계층 구조로 구성하는 효율적인 그래프 기반의 인덱싱 구조입니다. 그래프 분할 기법을 사용하여 벡터를 영역으로 나누기 때문에 가장 가까운 이웃을 더 빠르게 검색할 수 있습니다.
SPTAG is an efficient graph-based indexing structure that organizes vectors into a hierarchical structure. It uses graph partitioning techniques to divide the vectors into regions, allowing for a faster nearest-neighbor search.
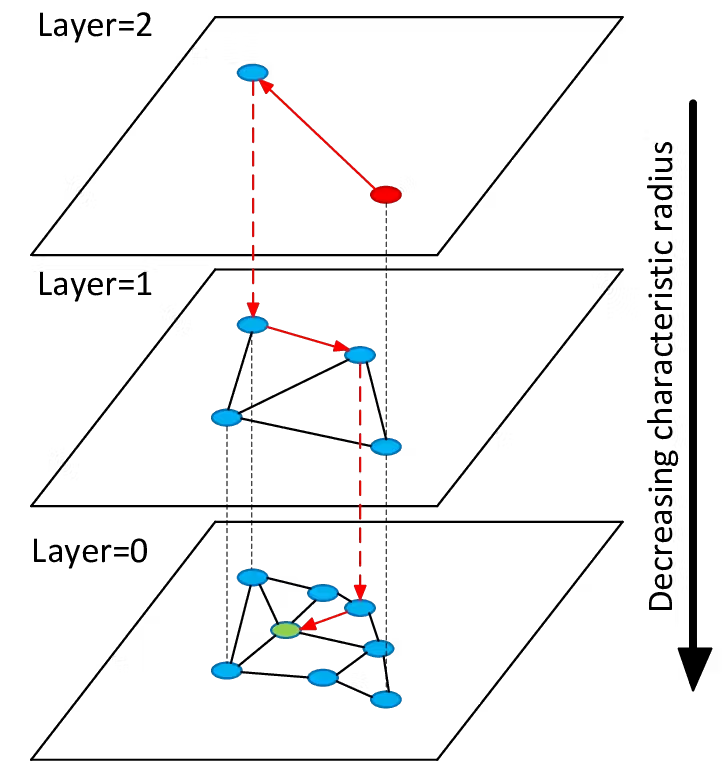
계층적, 탐색 가능한 작은 세계(HNSW) / Hierarchical Navigable Small World (HNSW)
HNSW는 그래프 기반의 알고리즘으로, 효율적인 검색을 위한 방법으로 벡터를 연결하여 계층적 그래프로 구성하는 방법입니다. 무작위 추출(randomization)과 지역 탐색(local exploration)을 조합하여 탐색 가능한 그래프 구조를 구축합니다.
HNSW is a graph-based algorithm that constructs a hierarchical graph by connecting vectors in a way that facilitates efficient search. It uses a combination of randomization and local exploration to build a navigable graph structure.
HNSW 그림. 출처 / Illustration of HNSW. Source
페이스북의 유사도 검색 알고리즘(Faiss) / Facebook’s similarity search algorithm (Faiss)
Faiss는 Facebook에서 밀집 벡터(dense vector)의 효율적 검색과 클러스터링을 위해 개발한 라이브러리입니다. 이 라이브러리는 정확도와 속도 간의 다양한 트레이드-오프(trade-off)에 최적화된 반전된 인덱스(inverted indices), 벡터 양자화(product quantization), 근사적인 거리 계산을 한 반전된 파일(IVFADC) 등의 다양한 인덱스 구조를 제공합니다.
Faiss is a library developed by Facebook for efficient similarity search and clustering of dense vectors. It provides various indexing structures, such as inverted indices, product quantization, and IVFADC (Inverted File with Approximate Distance Calculation), which are optimized for different trade-offs between accuracy and speed.
이러한 ANN 알고리즘들은 벡터 공간의 특성을 잘 살리고(leverage) 인덱싱 구조를 활용(explot)하여 검색을 빠르게 합니다. 가장 가까운 이웃을 포함할 가능성이 높은 영역(region)에 집중하여 검색 공간을 축소(reduce)함으로써 유사한 백터를 빠르게 찾을 수 있도록 합니다.
These ANN algorithms leverage the characteristics of the vector space and exploit indexing structures to speed up the search process. They reduce the search space by focusing on regions likely to contain nearest neighbors, allowing for fast retrieval of similar vectors.
벡터 유사도 검색의 사용 사례 / Use cases for Vector Similarity Search
백터 유사도 검색은 다양한 분야(domain)에서 수많은 예제와 사용 사례가 있습니다. 여기에서는 몇 가지 대표적인 사례를 살펴보겠습니다:
Vector similarity search has numerous examples and use cases across various domains. Here are some prominent examples:
추천 시스템 / Recommendation Systems
벡터 유사도 검색은 추천 시스템에서 중요한 역할을 합니다. 사용자와 항목(item)을 벡터로 표현함으로써, 유사한 사용자나 항목(item)들을 찾아내어 개인화된 추천을 가능하게 합니다. 예를 들어, 온라인 상거래(e-commerce) 분야에서는 사용자 선호도에 따라 제품을 추천하거나 협업 필터링(CF; collaborative filtering)으로 유사한 사용자를 찾는데 사용할 수 있습니다.
Vector similarity search plays a crucial role in recommendation systems. By representing users and items as vectors, similarity search helps find similar users or items, enabling personalized recommendations. For example, in e-commerce, it can be used to recommend products based on user preferences or to find similar users for collaborative filtering.
추천 시스템에서 벡터 유사도 검색을 사용하는 것을 보여주는 그림. 출처 / Illustration showing the use of vector similarity search in a recommendation system.Source
이미지 및 비디오 검색 / Image and Video Search
벡터 유사도 검색은 이미지 및 비디오 검색 어플리케이션에서 널리 사용합니다. 이미지나 비디오를 고차원의 특징 벡터(feature vector)로 표현함으로써, 시각적으로 유사한 콘텐츠를 찾는데 도움을 줍니다. 역방향 이미지 검색, 콘텐츠 기반 추천, 동영상 검색과 같은 작업들에 사용합니다.
Vector similarity search is widely used in image and video search applications. By representing images or videos as high-dimensional feature vectors, similarity search helps locate visually similar content. It supports tasks such as reverse image search, content-based recommendation, and video retrieval.
자연어 처리(NLP) / Natural Language Processing (NLP)
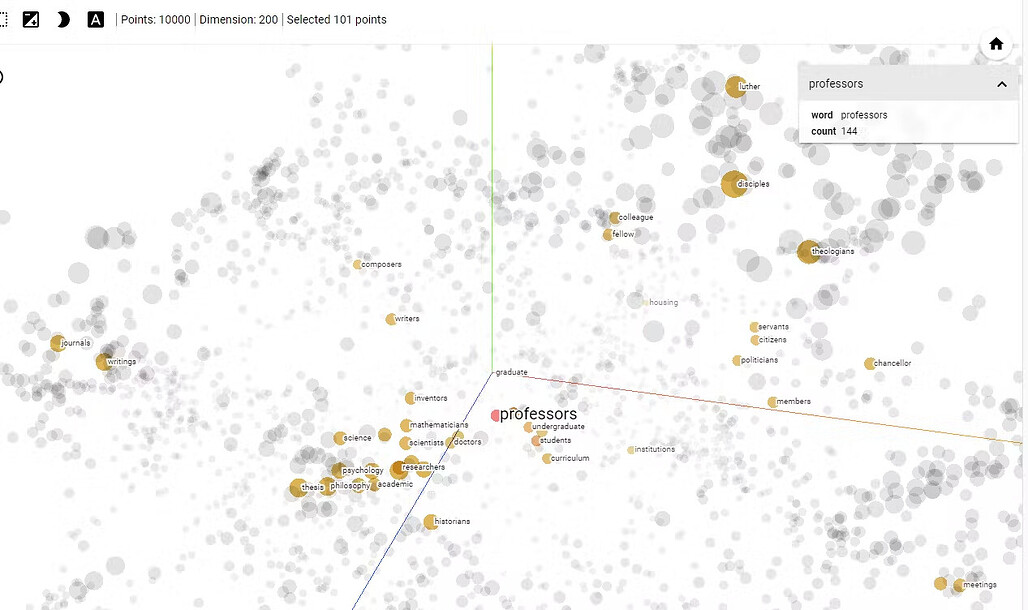
자연어 처리 분야에서 벡터 유사도 검색은 문서 유사도, 의미 검색(semantic search), 단어 임베딩 같은 작업에 사용합니다. Word2Vec이나 GloVe 같은 단어 임베딩 기법은 단어 또는 문서를 벡터로 변환하여 의미론적 뜻(semantic meaning)에 따라 유사한 문서 또는 단어를 효율적으로 검색할 수 있습니다.
In NLP, vector similarity search is employed for tasks like document similarity, semantic search, and word embeddings. Word embedding techniques like Word2Vec or GloVe transform words or documents into vectors, enabling efficient search for similar documents or words based on their semantic meaning.
단어 임베딩 시각화의 예. 출처 / Example of visualization of word embeddings. Source
이상 징후 탐지 / Anomaly Detection
벡터 유사도 검색은 이상 징후 탐지 어플리케이션에도 활용합니다. 데이터 포인트의 벡터를 정규 분포 또는 예상 분포와 비교하여 유사한 데이터를 식별할 수 있습니다. (전체 집단의) 다수(majority)로부터의 차이(deviations)로 이상 징후를 감지(consider)하여 사기 거래, 네트워크 침입 및 장비의 이상을 탐지하는데 도움을 줄 수 있습니다.
Vector similarity search is utilized in anomaly detection applications. By comparing the vectors of data points to a normal or expected distribution, similar vectors can be identified. Deviations from the majority can be considered anomalies, aiding in detecting fraudulent transactions, network intrusions, or equipment failures.
클러스터링 / Clustering
클러스터링 알고리즘은 종종 벡터 유사도 검색에 의존하여 유사한 데이터 포인트를 함께 그룹으로 묶습니다. 클러스터링 알고리즘은 가장 가까운 이웃 또는 가장 유사한 벡터를 식별함으로써, 데이터를 의미있는 그룹들로 효율적으로 분할(partition)할 수 있습니다. 이는 고객 세분화, 이미지 세분화(image segmentation) 및 유사한 인스턴스들끼리 묶어야 하는(grouping) 모든 종류의 작업에 유용합니다.
Clustering algorithms often rely on vector similarity search to group similar data points together. By identifying nearest neighbors or most similar vectors, clustering algorithms can efficiently partition data into meaningful groups. This is beneficial in customer segmentation, image segmentation, or any task that involves grouping similar instances.
Encord Annotate를 사용한 이미지 세분화 / Image Segmentation using Encord Annotate
게놈 시퀀싱 / Genome Sequencing
유전체학(genomics; 게놈학)에서, 벡토 유사도 검색은 DNA 서열을 분석하는데 도움이 됩니다. DNA 서열을 벡터로 표현하고 유사성 검색 알고리즘을 사용함으로써 연구자들은 효율적으로 순서(sequence)를 비교하고, 유전적 유사성을 식별하고, 유전적 변이(variation)를 발견할 수 있습니다.
In genomics, vector similarity search helps analyze DNA sequences. By representing DNA sequences as vectors and employing similarity search algorithms, researchers can efficiently compare sequences, identify genetic similarities, and discover genetic variations.
소셜 네트워크 분석 / Social Network Analysis
벡터 유사도 검색은 소셜 네트워크 분석 분야에서 사회적 연결이나 행동을 기반으로 유사한 사람들을 찾는데 사용합니다. 개개인을 벡터로 표현한 뒤 그들의 유사도를 측정함으로써, 영향력있는 사용자를 찾거나 소그룹(community) 찾기, 또는 잠재적 연결(potential connection)을 제안하는 작업에 도움을 줄 수 있습니다.
Vector similarity search is used in social network analysis to find similar individuals based on their social connections or behavior. By representing individuals as vectors and measuring their similarity, it assists in tasks such as finding influential users, detecting communities, or suggesting potential connections.
콘텐츠 필터링 및 검색 / Content Filtering and Search
벡터 유사도 검색은 콘텐츠 필터링 및 검색 어플리케이션에서 사용합니다. 유사도 검색은 문서, 기사 또는 웹 페이지를 벡터로 표현함으로써 질의 벡터(query vector)와의 유사도를 기반으로 관련 콘텐츠를 효율적으로 검색할 수 있게 해줍니다. 이는 뉴스 추천, 콘텐츠 필터링 및 검색엔진 등에서 유용합니다.
Vector similarity search is employed in content filtering and search applications. By representing documents, articles, or web pages as vectors, similarity search enables efficient retrieval of relevant content based on their similarity to a query vector. This is useful in news recommendations, content filtering, or search engines.
위에서 언급한 예시들은 다양한 분야(domain)에서 벡터 유사도 검색의 다양한 활용도(versatility)과 중요성(importance)를 보여주고 있습니다. 고차원 벡터와 유사도 기준(metric)의 기능을 활용(harness)함으로써, 벡터 유사도 검색으로 효율적인 정보 검색과 패턴 인식, 데이터 탐색 등을 용이하게 할 수 있습니다. 하지만, 현실 세계에서 벡터 유사도 검색을 적용할 때 마주칠 수 있는 문제들을 아는 것이 중요합니다.
The examples mentioned above highlight the versatility and importance of vector similarity search across different domains. By harnessing the capabilities of high-dimensional vectors and similarity metrics, this approach facilitates efficient information retrieval, pattern recognition, and data exploration. However, it is essential to acknowledge the challenges associated with employing vector similarity search in real-world applications.
구글의 벡터 유사도 검색 기술. 출처 / Google's vector similarity search technology. Source
벡터 유사도 검색의 걸림돌 / Vector Similarity Search Challenges
벡터 유사도 검색은 많은 이점을 제공하지만, 현실 세계에 적용하기 위해서는 몇 가지 걸림돌(challenge)들을 해결해야 합니다. 주요한 몇 가지 걸림돌들은 다음과 같습니다:
While vector similarity search offers significant benefits, it also presents certain challenges in real-world applications. Some of the key challenges include:
고차원 데이터 / High-dimensional Data
데이터의 차원이 증가함에 따라 차원의 저주(curse of dimensionality)는 주요한 걸림돌이 됩니다. 고차원 공간에서는 데이터의 희소성(sparsity)가 증가하게 되어 의미있는 유사도를 식별하기가 어렵습니다. 이로 인해 검색 성능이 저하되고 계산의 복잡도가 높아질 수 있습니다.
As the dimensionality of the data increases, the curse of dimensionality becomes a significant challenge. In high-dimensional spaces, the sparsity of data increases, making it difficult to discern meaningful similarities. This can result in degraded search performance and increased computational complexity.
확장성 / Scalability
대규모 데이터셋을 검색하는데는 연산 비용과 시간이 많이 들 수 있습니다. 데이터셋의 크기가 커지면 비교해야 할 벡터의 수가 증가하기 때문에, 검색 프로세스는 더욱 어려워집니다. 벡터 유사도 검색과 관련한 확장성 문제를 해결하기 위해서는 효율적인 인덱싱 구조와 알고리즘이 필요합니다.
Searching through large-scale datasets can be computationally expensive and time-consuming. As the dataset size grows, the search process becomes more challenging due to the increased number of vectors to compare. Efficient indexing structures and algorithms are necessary to handle the scalability issues associated with vector similarity search.
거리 측정 기준 고르기 / Choice of Distance Metric
벡터 유사도 검색에서는 적절한 거리 측정 지표(metric)를 선택하는 것이 중요합니다. 데이터의 특성과 적용 분야에 따라 서로 다른 거리 측정 지표는 서로 다른 결과를 야기(yield)할 수 있습니다. 원하는 유사도의 개념(notion of similarity)에 맞는 올바른 지표를 고르는 일은 결코 쉬운(non-trivial) 일이 아니므로 신중하게 고려해야 합니다.
The selection of an appropriate distance metric is crucial in vector similarity search. Different distance metrics may yield varying results depending on the nature of the data and the application domain. Choosing the right metric that captures the desired notion of similarity is a non-trivial task and requires careful consideration.
인덱싱 및 저장소 요구사항 파악하기 / Indexing and Storage Requirements
고차원 공간에서 빠른 검색을 위해서는 효율적인 인덱싱 구조가 필수적입니다. 이러한 인덱스를 구축 및 유지하려면 스토리지 오버헤드가 발생할뿐만 아니라 연산 자원도 필요로 합니다. 인덱싱의 효율성과 스토리지의 요구 사항 사이의 균형을 맞추는 것(trade-off)은 벡터 유사도 검색에 있어서 어려운 과제입니다.
Efficient indexing structures are essential to support fast search operations in high-dimensional spaces. Constructing and maintaining these indexes can incur storage overhead and necessitate computational resources. Balancing the trade-off between indexing efficiency and storage requirements is a challenge in vector similarity search.
정확도와 효율성 사이의 균형 맞추기 / The trade-off between Accuracy and Efficiency
많은 근사 최인접 이웃(ANN; Approximate Nearest Neighbor) 알고리즘은 더 빠른 검색 성능을 위해 정확도를 어느 정도 희생합니다. 검색의 정확도와 계산 효율성 사이의 적절한 균형을 맞추는 것은 매우 중요하며, 이는 어플리케이션의 요구사항과 제약 조건에 따라 달라집니다.
Many approximate nearest neighbor (ANN) algorithms sacrifice a certain degree of accuracy to achieve faster search performance. Striking the right balance between search accuracy and computational efficiency is crucial and depends on the specific application requirements and constraints.
데이터 분포 및 쏠림 / Data Distribution and Skewness
데이터 분포(distribution)와 쏠림(skewness)은 벡터 유사도 검색 알고리즘의 효율에 영향을 미칠 수 있습니다. 데이터의 분포가 균일하지 않거나(non-uniform), 데이터가 불균형(imbalance)하면 검색 결과가 편향(bias)되거나 질의 성능이 최적화되지 않을 수(suboptimal) 있습니다. 데이터의 쏠림을 처리하고 다양한 데이터 분포에서도 견고(robust)한 알고리즘을 설계하는 것은 어려운 과제입니다.
The distribution and skewness of the data can impact the effectiveness of vector similarity search algorithms. Non-uniform data distributions or imbalanced data can lead to biased search results or suboptimal query performance. Handling data skewness and designing algorithms that are robust to varying data distributions pose challenges.
결과의 설명 가능성 / Interpretability of Results
벡터 유사도 검색은 주로 수학적 유사도를 측정한 값을 기반으로 유사한 벡터를 식별하는데 중점을 둡니다. 이는 많은 어플리케이션에서 효과적일 수 있지만, 결과를 설명하는 것(interpretability)은 어려울 수 있습니다. 두 벡터가 유사한 것으로 판단(consider)한 이유를 이해하고, 결과에서 의미있는 인사이트를 도출하려면 추가적인 후처리(post-processing)와 분야별 전문지식(domain-specific knowledge)이 필요할 수 있습니다.
Vector similarity search primarily focuses on identifying similar vectors based on mathematical similarity measures. While this can be effective for many applications, the interpretability of the results can sometimes be challenging. Understanding why two vectors are considered similar and extracting meaningful insights from the results may require additional post-processing and domain-specific knowledge.
벡터 유사도 검색 문제의 해결방법 / How to Solve Vector Similarity Search Challenges
다음은 고차원 데이터 처리, 거리 측정 기준 선택, 인덱싱 및 저장소 요구사항 등, 위에서 나열한 문제들을 해결하는데 사용할 수 있는 몇 가지 접근 방식입니다.
Here are some approaches you can use to solve the challenges listed above, including handling high-dimensional data, the choice of distance metrics, and indexing and storage requirements.
고차원 데이터 / High-Dimensional Data
차원의 저주 / Dimensionality Reduction
주성분 분석(PCA) 또는 t-SNE 등의 기법들을 사용하여 의미있는 유사도를 보존하면서 데이터의 차원을 줄입니다.
Apply techniques like Principal Component Analysis (PCA) or t-SNE to reduce the dimensionality of the data while preserving meaningful similarities.
특징(feature) 선택: 가장 관련이 높은 특징(feature)을 고르고 유지하여 차원을 줄이고 차원의 저주를 완화합니다.
Feature selection: Identify and retain only the most relevant features to reduce the dimensionality and mitigate the curse of dimensionality.
데이터 전처리 / Data preprocessing
데이터를 정규화(normalize)하거나 규모(scale)를 조절하여 특징(feature)의 크기(scale)가 유사도 계산에 끼치는 영향을 줄입니다. 이는 입력 데이터를 적절히 준비하고, 이상값(outlier)과 결측치(missing value)를 처리하며, 입력 데이터의 전반적인 품질을 개선하기 위한 것으로, PCA에서 특히 중요한 절차입니다.
Normalize or scale the data to alleviate the impact of varying feature scales on similarity computations. This is especially important in PCA to ensure that the input data is appropriately prepared, outliers and missing values are handled, and the overall quality of the input data is improved.
거리 측정 기준 고르기 / Choice of Distance Metric
분야에 특화된 거리 측정 기준 / Domain-specific metrics
특정 분야(specific domain) 또는 어플리케이션의 요구사항에 맞는 거리 측정 기준(metric)을 설계하거나 선택하여 원하는 유사도의 개념(notion of similarity)을 보다 정확하게 측정할 수 있도록 합니다.
Design or select distance metrics that align with the specific domain or application requirements to capture the desired notion of similarity more accurately.
적응형 거리 측정 기준 / Adaptive distance metrics
데이터의 특성(characteristic)에 따라 유사도 측정을 동적(dynamically)으로 조정하는 적응형 또는 학습에 기반한 거리 측정 기준들을 찾아보세요.
Explore adaptive or learning-based distance metrics that dynamically adjust the similarity measurement based on the characteristics of the data.
인덱싱 및 저장소 요구사항 / Indexing and Storage Requirements
균형 찾기 전략 / Trade-off Strategies
적절한 인덱싱 구조와 압축 기법을 선택하여 인덱싱의 효율성과 저장소 요구사항 사이의 균형을 맞출 수 있도록 합니다.
Balance the trade-off between indexing efficiency and storage requirements by selecting appropriate indexing structures and compression techniques.
근사 인덱싱 / Approximate indexing
저장 공간과 검색의 정확도, 그리고 질의의 효율성 사이의 절충점을 찾을 수 있는 근사(approximate) 인덱싱 방식을 사용(adopt)해보세요.
Adopt approximate indexing methods that provide trade-offs between storage space, search accuracy, and query efficiency.
신경망 해싱 / Neural Hashing
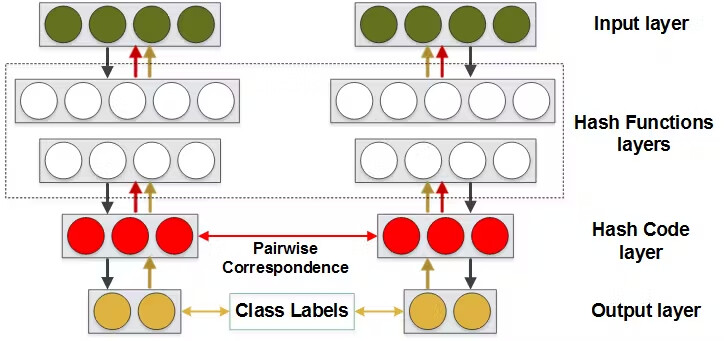
신경망 해싱은 벡터 유사도 검색의 문제를, 특히 정확도와 속도 측면에서 해결할 수 있는 기법입니다. 신경망 해싱을 활용(leverage)하여 고차원 벡터를 표현하는 간결한 바이너리 코드(binary code)를 생성하여, 효율적이고 정확한 유사도 검색을 가능케 합니다.
Neural hashing is a technique that can be employed to tackle the challenges of vector similarity search, particularly in terms of accuracy and speed. It leverages neural networks to generate compact binary codes that represent high-dimensional vectors, enabling efficient and accurate similarity searches.
신경망 해싱의 예시. 출처 / An example of neural network hashing. Source
신경망 해싱의 동작 원리 / Neural Hashing Mechanism
신경망 해싱은 다음 세가지 단계로 동작합니다:
Neural hashing works in three phases:
학습 단계 / Training Phase
학습 단계에서는 신경망 모델이 고차원 벡터를 간결한 바이너리 코드로 변환하는 변환 함수(mapping function)를 학습합니다. 이러한 변환 함수는 원본 벡터들 간의 유사도를 보존하도록 합니다.
In the training phase, a neural network model is trained to learn a mapping function that transforms high-dimensional vectors into compact binary codes. This mapping function aims to preserve the similarity relationships between the original vectors.
바이너리 코드 생성 단계 / Binary Code Generation
신경망이 학습되면, 이를 사용하여 데이터셋 내의 벡터들을 가지고 바이너리 코드를 생성합니다. 각각의 벡터는 바이너리 코드로 인코딩(encode)되며, 이 때 바이너리 코드의 각 비트들은 특정한 특징(feature) 또는 벡터의 특징(characteristic)을 표현합니다.
Once the neural network is trained, it is used to generate binary codes for the vectors in the dataset. Each vector is encoded as a binary code, where each bit represents a specific feature or characteristic of the vector.
유사도 검색 단계 / Similarity Search
유사도 검색 단계에서는 원래의 고차원 벡터 대신 바이너리 코드들을 비교합니다. 이 때, 바이너리 코드들 간의 비교는 고차원 벡터들 간의 비교에 비해서 (유사도를) 계산하는 비용이 저렴하기 때문에 효율적으로 검색을 할 수 있습니다.
During the similarity search phase, the binary codes are compared instead of the original high-dimensional vectors. This enables efficient search operations, as comparing binary codes is computationally inexpensive compared to comparing high-dimensional vectors.
신경망 해싱은 간결한 바이너리 코드로 데이터의 차원을 줄임으로써 효율성을 높이고 대규모 데이터셋의 확장성을 향상시킵니다. 이는 신경망을 통해 근본적인(underlying) 유사도를 포착하여 정확하게 유사도를 보존하고, 정확한 유사도 검색을 용이하게 합니다.
Neural hashing offers improved efficiency by reducing the dimensionality of data with compact binary codes, enhancing scalability for large-scale datasets. It ensures accurate similarity preservation by capturing underlying similarities through neural networks, facilitating precise similarity searches.
신경망 해싱 기법은 저장소를 작게(compact)하여, 저장소 요구사항을 줄임으로써 보다 효율적인 데이터 검색을 가능케 합니다. 사용자는 바이너리 코드의 길이를 변경함으로써 검색의 정확도와 계산의 효율성 간의 균형을 유연하게 맞출 수 있습니다. 신경망 해싱은 텍스트와 이미지 등의 다양한 분야(domain)에 적용할 수 있어 다양한 어플리케이션에 다용도로 사용할 수 있습니다.
The technique enables compact storage, reducing storage requirements for more efficient data retrieval. With flexibility in trade-offs, users can adjust binary code length to balance search accuracy and computational efficiency. Neural hashing is adaptable to various domains, such as text and images, making it versatile for different applications.
컴퓨터 비전(CV) 분야에서의 벡터 유사도 검색 사용 사례 / How Vector Similarity Search can be used in Computer Vision
벡터 유사도 검색은 다양한 컴퓨터 비전 어플리케이션에서 매우 중요하며, 효율적인 객체 탐지, 인식 및 검색을 가능하게 합니다. 이렇게 이미지를 고차원 특징 벡터로 표현함으로써, 벡터 유사도 검색 알고리즘은 대규모 데이터셋에서 유사한 이미지를 찾을(locate) 수 있게 하는 등, 여러가지 실질적인 이점을 제공합니다.
Vector similarity search is crucial in various computer vision applications, enabling efficient object detection, recognition, and retrieval. By representing images as high-dimensional feature vectors, vector similarity search algorithms can locate similar images in large datasets, leading to several practical benefits.
객체 탐지 / Object Detection
벡터 유사도 검색은 관심있는 객체(object of interest)가 포함된 유사한 이미지를 찾음으로써 객체 탐지에 도움을 줄 수 있습니다. 예를 들어, 시스템은 사전에 학습(pre-trained)된 딥러닝 모델을 사용하여 이미지에서 특징 벡터(feature vector)를 추출(extract)할 수 있습니다. 이렇게 추출된 벡터들은 벡터 유사도 검색 비법을 사용하여 인덱싱합니다. 실행 시(runtime)에 새로운 이미지가 입력되면, 그 이미지의 특징 벡터를 인덱싱된 벡터들과의 비교를 통해 유사한 객체를 갖는 이미지들을 찾을(identify) 수 있습니다. 이렇게 실시간으로 물체를 감지하고 시각적 검색(visual search)과 같은 어플리케이션을 지원할 수 있습니다.
Vector similarity search can aid in object detection by finding similar images that contain objects of interest. For example, a system can use pre-trained deep-learning models to extract feature vectors from images. These vectors can then be indexed using vector similarity search techniques. During runtime, when a new image is provided, its feature vector is compared to the indexed vectors to identify images with similar objects. This can assist in detecting objects in real-time and supporting applications like visual search.
![]() Encord에서 제공하는 객체 검색과 그 사용 사례에 대한 가이드를 읽어보세요..
Encord에서 제공하는 객체 검색과 그 사용 사례에 대한 가이드를 읽어보세요..
Read our guide on object detection and its use cases to find out more.
이미지 검색 / Image Retrieval
벡터 유사도 검색은 효율적인 콘텐츠 기반의 이미지 검색을 가능하게 합니다. 이미지를 고차원의 특징 벡터로 변환함으로써 시각적으로 유사한 콘텐츠가 있는 이미지들을 빠르게 식별할 수 있습니다. 이는 사용자가 이미지를 입력하고 데이터베이스에서 시각적으로 유사한 이미지를 검색하는 역방향 이미지 검색(reverse image search)과 같은 어플리케이션에서 특히 유용합니다. 이러한 기능은 이미지 검색 엔진, 이미지에 기반한 제품 추천, 구조화(organization)를 위한 이미지 클러스터링 등의 어플리케이션 등에서 사용할 수 있습니다.
Vector similarity search allows for efficient content-based image retrieval. By converting images into high-dimensional feature vectors, images with similar visual content can be identified quickly. This is particularly useful in applications such as reverse image search, where users input an image and retrieve visually similar images from a database. It enables applications like image search engines, product recommendations based on images, and image clustering for organizations.
이미지 인식 / Image Recognition
벡터 유사도 검색은 입력 이미지의 특징 벡터를 이미 갖고있는(known) 이미지들의 인덱싱된 벡터들과 비교하여 이미지 인식 작업을 용이하게 합니다. 이러한 기능은 이미지 분류(image classification) 및 이미지 유사도 순위 지정(image similarity ranking) 등에 사용합니다.
Vector similarity search facilitates image recognition tasks by comparing feature vectors of input images with indexed vectors of known images. This aids in tasks like image classification and image similarity ranking.
예를 들어, 이미지 인식 시스템에서는 질의 이미지(query image)의 특징 벡터를 알려진 분류(class) 또는 이미 인덱싱된 이미지들의 벡터와 비교하여 가장 유사한 분류(class) 또는 이미지를 찾습니다. 이러한 접근 방식은 얼굴 인식이나 장면 인식, 이미지 분류(image categorization)과 같은 어플리케이션에 사용됩니다.
For example, in image recognition systems, a query image's feature vector is compared to the indexed vectors of known classes or images to identify the most similar class or image. This approach is employed in applications like face recognition, scene recognition, and image categorization.
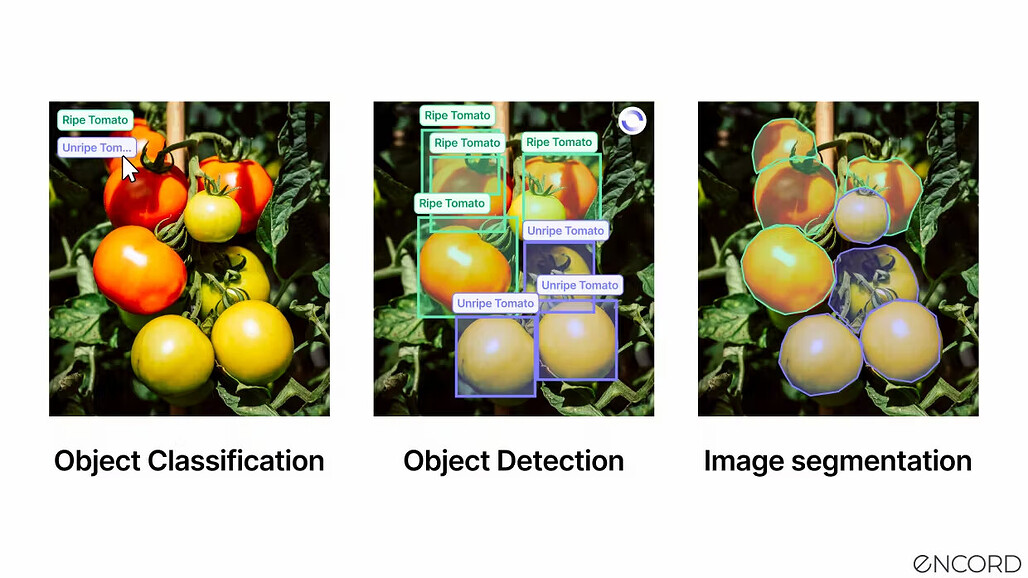
이미지 세분화 / Image Segmentation
벡터 유사도 검색은 이미지 세분화(image segmentation) 작업 시에도 도움이 될 수 있습니다. 이미지 세분화는 이미지를 의미있는 영역이나 객체로 분할(partition)하는 것이 목표인 작업(task)입니다. 이미지의 조각(patch) 또는 수퍼픽셀(superpixel; 유사성을 띈 인접한 픽셀들을 모은 것, 참고)의 특징 벡터들을 비교하여 유사한 영역을 그룹화할 수 있습니다. 이렇게 하면 객체 간의 경계(boundary)를 식별하거나 유사한 시각적 특성(visual characteristic)을 가진 영역을 결정함으로써 객체 분할(object segmentation)이나 이미지 주석(image annotation) 같은 작업 시에 도움이 됩니다.
Vector similarity search can assist in image segmentation tasks, where the goal is to partition an image into meaningful regions or objects. Similar regions can be grouped by comparing feature vectors of image patches or superpixels. This aids in identifying boundaries between objects or determining regions with similar visual characteristics, supporting tasks like object segmentation and image annotation.
벡터 유사도 검색 요약 / Vector Similarity Search Summary
벡터 유사도 검색은 고차원 공간에서 유사한 데이터 포인트들을 찾는데 사용하는 머신러닝의 핵심 기법(vital technique)입니다. 이는 추천 시스템이나 이미지 및 비디오 검색, 자연어 처리, 클러스터링 등에서 매우 중요합니다. 이 때 고차원 데이터를 다루거나 확장성, 거리 측정 기준 선택 방법 및 저장소 요구사항 등의 과제가 있습니다.
Vector similarity search is a vital technique in machine learning used to find similar data points in high-dimensional spaces. It is crucial for recommendation systems, image and video search, NLP, clustering, and more. Challenges include high-dimensional data, scalability, choice of a distance metric, and storage requirements.
이를 해결하기 위한 방법으로 차원 축소, 인덱싱 구조, 적응형 거리 측정 기준 및 신경망 해싱 등이 있습니다. 컴퓨터 비전 분야에서는 벡터 유사도 검색은 객체 탐지, 이미지 검색과 인식, 세분화에 사용하여 효율적인 검색과 빠른 감지, 정확한 인식을 가능하도록 합니다. 머신러닝 어플리케이션을 향상시키고 사용자 경험을 개선하기 위해서는 벡터 유사도 검색을 완전히 익히는(mastering) 것이 필수적입니다.
Solutions involve dimensionality reduction, indexing structures, adaptive distance metrics, and neural hashing. In computer vision, vector similarity search is used for object detection, image retrieval, recognition, and segmentation. It enables efficient retrieval, faster detection, and accurate recognition. Mastering vector similarity search is essential for enhancing machine learning applications and improving user experiences.
주요 요점 정리 / Key Takeaways
- 벡터 유사도 검색은 수많은 머신러닝 어플리케이션들에 필수적이며, 정확하고 효율적인 데이터 분석을 가능하게 합니다.
- Vector similarity search is essential for numerous machine learning applications, enabling accurate and efficient data analysis.
- 고차원의 데이터 및 확장성 등의 문제들을 극복하기 위해서는 차원 축소 및 인덱싱 구조와 같은 기법들이 필요합니다.
- Overcoming challenges like high-dimensional data and scalability require techniques such as dimensionality reduction and indexing structures.
- 적응형 거리 측정 기준과 근사 최인접 이웃 알고리즘(ANN)은 검색의 정확도와 효율성을 향상시킬 수 있습니다.
- Adaptive distance metrics and approximate nearest-neighbor algorithms can enhance search accuracy and efficiency.
- 컴퓨터 비전 분야에서 벡터 유사도 검색은 객체 탐지, 이미지 검색, 인식, 세분화를 지원하여 고급 시각적 이해 및 해석을 가능하게 합니다.
- In computer vision, vector similarity search aids in object detection, image retrieval, recognition, and segmentation, enabling advanced visual understanding and interpretation.
![]() 주의: 아래 내용은 Encord 서비스의 광고입니다. 파이토치 한국 사용자 모임은 Encord의 서비스와 어떠한 직/간접적인 관련이 없으며, 콘텐츠 번역을 허락해주신 것에 대한 감사의 의미로 아래 내용을 함께 번역하여 제공하고 있음을 알려드립니다.
주의: 아래 내용은 Encord 서비스의 광고입니다. 파이토치 한국 사용자 모임은 Encord의 서비스와 어떠한 직/간접적인 관련이 없으며, 콘텐츠 번역을 허락해주신 것에 대한 감사의 의미로 아래 내용을 함께 번역하여 제공하고 있음을 알려드립니다.
컴퓨터 비전 프로젝트의 품질, 속도, 정확성을 자동화하고 개선할 준비가 되셨나요?
Ready to automate and improve the quality, speed, and accuracy of your computer vision projects?
Encord 무료 평가판에 등록하세요: 세계 최고의 컴퓨터 비전팀에서 사용하는 컴퓨터 비전용 액티브 러닝 플랫폼입니다.
Sign-up for an Encord Free Trial: The Active Learning Platform for Computer Vision, used by the world’s leading computer vision teams.
AI가 지원하는 라벨링, 모델 학습 및 진단, 데이터셋의 오류와 편향을 찾고 수정할 수 있는, 모든 기능이 하나로 포함된 협업형 액티브 러닝 플랫폼을 사용하여 상용급 AI를 더 빠르게 얻을 수 있습니다. 지금 Encord를 무료로 사용해보세요.
AI-assisted labeling, model training & diagnostics, find & fix dataset errors and biases, all in one collaborative active learning platform, to get to production AI faster. Try Encord for Free Today.
Encord의 최신 소식을 받고 싶으신가요?
Want to stay updated?
- Encord의 Discord 채널에 가입하여 채팅하고 소통해보세요.
- Join our Discord channel to chat and connect.